As you may have noticed, this has turned into a linkblog. Blame my job. Blame one of your fellow readers for alerting me of the job’s existence.

Andrew Gelman asks Do college football results impact the election?

Darryl Yong in the Notices of the AMS: Adventures in teaching: A professor goes to high school to learn about teaching math?

Technology Review reports on Univfy, a startup answering the question of what your chances of conceiving a baby via IVF are.

David Talbot at Technology Review asks what google knows about the presidential race.

Papercraft sculptures based on Byrne’s Euclid.

Donald Saari, who works on the theory of voting, goes to a fourth grade classroom. The fourth graders are surprisingly smart.

Rick Wicklin simulates playing craps with unfair dice.

StubHub has a data blog. The first post examines the correlations between preference in sport (baseball vs. football) and political party (Democratic vs. Republican).

Integrals don’t have anything to do within discrete math, do they?. By Mark Kayll, winner of the MAA’s Allendoerfer prize for articles published in Mathematics Magazine.

Allen Downey has a rough draft of his book Think Bayes.

Steven Strogatz has written a brief, nontechnical introduction to catastrophe theory for the New York Times.

Probability and game theory in The Hunger Games.

Daniel Engber asks how the Internet fell in love with a stats class cliche. (You know which one.)

Shapley’s layman’s account of the general principles of game theory. (Was anyone else surprised, when the Nobel was announced, to learn that Shapley was still alive?)

The Daily Show with Nate Silver.

Brian Hayes writes about sphere packing for American Scientist and talks about how he made the images for his blog.

David Barber has written a textbook, freely available online, entitled Bayesian reasoning and machine learning.

James Tanton asked in a tweet a few days ago: “If a,b,c are the sides of a right triangle with hypotenuse c, what is the largest possible value of a/c + b/c?”

The answer is the square root of 2. But how to see this?

Well, without loss of generality we can assume c = 1. So we want to know, if a and b are the sides of a right triangle with hypotenuse 1, what is the largest possible value of a + b?

Now a and b are, respectively, cos θ and sin θ for some acute angle θ… so we want to maximize over acute angles $\theta$. But how? Differentiate? That sounds like work.

Take a look at the picture below. Imagine moving the upper right corner of the (black) right triangle along the (black) circular arc; we’re looking for the point where the sum of the lengths of the legs is maximized. But now say we can move the upper right corner of the right triangle wherever we want it. As long as we stay along one of those red lines — which have slope -1, i. e. make a 45-degree angle with each axis, the sum of the leg lengths stays constant!

As we move the upper right corner along the circular arc, the sum of the leg lengths is maximized when it’s locally constant — that is, when the circle is tangent to one of those lines. The red lines make a 45-degree angle with the coordinate axes; the optimal hypotenuse will be perpendicular to them, also making a 45-degree angle with the coordinate axes. The optimal right triangle is the one with 45-degree angles… so if its hypotenuse is 1, its legs are each , and their sum . (This is not the triangle in the plot — the triangle in the plot is in the 3-4-5 ratio. The sum of its legs is 1.4, not much short of optimality.)

This is, secretly, the principle behind using Lagrange multipliers to maximize a function subject to a constraint. It’s also much easier to see than to explain.

David Spiegelhalter suggests that older should mean bolder. Lethal risks are less dangerous if you’re old, because you have less to lose.

Bill Watterson thought of this too. (I thanks Michael Yingling’s Calvin and Hobbes search engine for helping me find this.)

Freakonomics Q&A with Nate Silver.

A new geometric minimal composition every day.

forecasting the Presidential election using regression, simulation, or dynamic programming.

Best practices for scientific computing. Worth reading if you are, like so many scientists, a self-taught software developer. (Actually, very little of what’s said here is specific to scientific computing.)

Stein’s paradox in statistics, by Bradley Efron and Carl Morris.

The Simons Foundation has an article by Erica Klarreich, Getting Into Shapes: From Hyperbolic Geometry to Cube Complexes and Back”, on Thurston’s geometrization conjecture.

Peter Norvig’s spelling corrector in 25 lines of Python

James Tanton asks: “An old question: Triang nmbrs:1,3,6,10,15,.. For every triangular nmbr is there a second larger triang nmbr so that their product is square?”

Answer: yes! I thought “hey, this is a question I can answer in my head!” but didn’t get further than noticing that 1 times 36 is 36. Then I got home and wrote some Python. (You’ll probably see this blog’s language of choice shifting from R to Python, mostly because I’m using Python at work and this gives me a chance to practice.)

import math

def tri(n):
    return n*(n+1)/2

def is_square(integer):
    root = math.sqrt(integer)
    if int(root + 0.5) ** 2 == integer:
        return True
    else:
        return False

def next_tri(n, m):
    z = False
    i = 0
    while ((not z) and (i < m)):
        i += 1
        if is_square(tri(n)*tri(n+i)):
            return n+i
    return 0

def answers(n, m):
    list = [0]*n
    for i in range(1, n+1):
        list[i-1] = next_tri(i, m)
    return list

The first function here, tri, outputs triangular numbers; the second tells you if its input is a square, and is taken from this Stackoverflow answer. next_tri is where the “magic” happens; it outputs the index of the first triangular number k greater than n such that tri(n)*tri(k) is a square. But since this loop may, a priori, be infinite, we cut this off at k = n+m. If none of tri(n)tri(n+1), tri(n)tri(n+2), …, tri(n)tri(n+m) are square, it outputs 0. Finally, calling answers(n,m) outputs the list answers(1,m), answers(2,m), …, answers(n,m).

If you call answers(10, 1000) you get the output

[8, 24, 48, 80, 120, 168, 224, 49, 360, 440].

So, for example, tri(1) tri(8) = (1)(36) = 36 is square, namely 6²; tri(2) tri(24) = (3)(300) = 900 = 30²; and so on. If you ignore the eighth element of this list and stare for a moment, you start to see a quadratic! Namely,

appears to be a square. And in fact we can write

This is an identity that’s not hard to prove, and answers Tanton’s question in the affirmative, but I think it’s hard to discover without computation. Of course you could do the computation by hand, but it’s 2012.

But this identity tells us that — and this is true, but 288 is not the smallest solution to the problem that Tanton originally posed. In fact the computer search gives 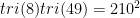. When do smaller solutions exist?

Steven Strogatz digs up a clip about the birthday problem on the Tonight Show.

UK MPs have weak ability to do basic statistics. (I wonder if the same would be true of US congresspeople.)

In the Guardian, is it Mitt Romney’s fault, if he loses?, with regressions based on approval ratings.

Some data on job listings for data scientists