Weekly links for September 30

The Mathematics Behind xkcd: A conversation with Randall Munroe.

Carl Bialik at the Wall Street Journal writes about which voters are the most powerful in US presidential elections.

Forget your fancy data science: try overkill analytics.

Dynamic pricing for drinks, from Wired via io9.

Identification of fraudulent elections. (Basically, if a region has abnormally high turnout and most of the votes go to a single candidate, be suspicious!)

Call me maybe and the prisoner’s dilemma.

Andrew G Haldane: The dog and the frisbee, via John D. Cook (Cook points out that you want to use a simple model when possible, because complicated models are less robust.)

Optimizing your baggage claim experience.

What is the optimal way to find a parking spot?

Weekly links for September 23

An analysis of (leaked) PIN numbers from DataGenetics

Friends you can count on, from Steven Strogatz’ current New York Times series “Me, Myself, and Math”.

The Toolbox, the first episode of Samuel Hansen’s 8-episode audio series featuring stories from the world of mathematics.

Terry Tao has written a probablistic heuristic justification of the abc conjecture.

This is old news, but Stanford has an archive of Knuth video lectures.

(Oh, hey, I got a job! I start tomorrow.)

Triangular numbers between square numbers

James Tanton asked on Twitter:

As there are “more” triang nmbrs than sq nmbrs http://www.jamestanton.com/?p=1009 let f(N) = nmbr triangs >= N^2 but < (N+1)^2. Curious:What graph like?

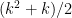The $k$ th triangular number is about $k^2/2$ (more precisely, it’s $(k^2+k)/2$ .) So there are about $\sqrt{2} n$ triangular numbers less than 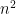$n^2$ . Therefore, “on average”, in each interval $[N^2, (N+1)^2)$ there are $\sqrt{2}$ triangular numbers.

For example, in the interval [9, 16) there are two triangular numbers, namely 10 and 15; this is f(3). In the interval [16, 25) there is one triangular number, namely 21; this is f(4).

Let’s write down an explicit formula for f(n). Let g(x) be the number of triangular numbers less than x. To figure this out, I’ll introduce a function t(x), which takes as input x and outputs the index of x in the triangular-number sequence. For example, t(10) = 4, t(15) = 5. But we also want to be able to compute, say, t(12). But that’s fine! t(n) is just the inverse of the function which takes n to the nth triangular number, the function $n \to (n^2+n)/2$ ; in particular, solving the quadratic,

$t(n) = {\sqrt{8n+1}-1 \over 2}.$

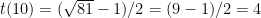So $t(10) = (\sqrt{81}-1)/2 = (9-1)/2 = 4$ ; $t(12) = (\sqrt{97}-1)/2 \approx 4.42$ .

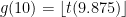Next we write g(x) in terms of t(x). It’s tempting to say that g(x) = \lfloor t(x) \rfloor, but it’s not. t(10) = 4, for example, but we want g(10) = 3. We’ll say that $g(x) = \lfloor t(x-1/8) \rfloor$ — we’ll only need this formula to work when x is an integer. So, for example, $g(10) = \lfloor t(9.875) \rfloor$ , and the index of 9.875 in the triangular number sequence, whatever that means, is between 3 and 4. 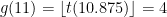But $g(11) = \lfloor t(10.875) \rfloor = 4$ .

Why the constant 1/8? Because

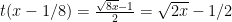
$t(x-1/8) = {\sqrt{8x}-1 \over 2} = {\sqrt{2x}} - {1/2}$

which makes the formula marginally easier to write.

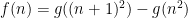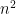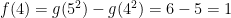Finally $f(n) = g((n+1)^2) - g(n^2)$ . Take the number of triangular numbers less than $(n+1)^2$ , and subtract the number less than $n^2$ , and you get the number in the interval in between. For example $g(5^2) = \lfloor \sqrt{50} - 1/2 \rfloor = 6$ ; there are 6 triangular numbers less than 25, namely 1, 3, 6, 10, 15, and 21. And $g(4^2) = \lfloor \sqrt{32} - 1/2 \rfloor = 5$ . Thus $f(4) = g(5^2) - g(4^2) = 6-5 = 1$ , indicating the triangular number 21. So at long last we have the formula

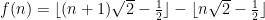$f(n) = \lfloor (n+1) \sqrt{2} - {1 \over 2} \rfloor - \lfloor n \sqrt{2} - {1 \over 2} \rfloor$ .

In particular the arguments of these two floor functions differ by $\sqrt{2}$ , which is between 1 or 2, so f(n) is always either 1 or 2. The graph that Tanton asked about is below.

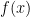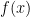You can see some hints of periodicity in the function; for example, from a quick glance at the graph it might look like $f(x)$ has period 12, each period containing five 2s and seven 1s. But this can’t hold, not unless $\sqrt{2} = 17/12$ . In fact $f(x)$ can’t be periodic, because $\sqrt{2}$ is irrational.

Weekly links for September 16

Is an auction the best way to solve the roommate/rent dilemma? At Freakonomics, referring to The rent is too damn fair! by Michael Jancsy et al. The title is a reference to “The Rent Is Too Damn High!”, political party and e-book by Matt Yglesias. (Conflict-of-interest disclosure: I know Jancsy, and I went to college with Yglesias’ wife.)

Larry Wasserman writes on Hunting for Manifolds. Given data that are close to some manifold, how do we estimate the underlying manifold?

RAND’s presidential election poll features some unorthodox methodology, including asking the same people repeatedly and asking them explicitly for the percentage chance that they’ll vote.

Brian Hayes explains the abc conjecture. (He’s done this before.)

Steven Strogatz has a new series of math blog posts at the New York Times.

John Allen Paulos on Letterman. (Presumably from 1988.)

Life expectancy doesn’t measure how long you’re expected to live.

Howard Wainer writes of the most dangerous equation: (ignorance of) what I call the “square root law”. (From Wainer’s website for his intro stat course which contains some other interesting links.)

Austin Mohr has created Spacebook, a searchable database of topological spaces inspired by Counterexamples in Topology.

Handouts from Geometry and the Imagination, a summer workshop by John Conway, Peter Doyle, Jane Gilman and Bill Thurston in 1991.

Animation of Bruce Springsteen’s diffusion. (For The Girlfriend and my father. The Girlfriend is from Arkansas, so this is a good excuse to point to the Walmart diffusion animation as well.)

An interesting visualization of prime factorization.

The best video I’ve ever seen on combinatorial explosion.

10 Turkish lira

The 10 Turkish lira note has math on it. I was inordinately amused by this when I discovered it yesterday, totally by accident when my girlfriend was showing me some money she picked up on a layover in Istanbul. In particular it includes a picture of Cahit Arf, whose work I am not familiar with but who appears to be one of the great Turkish mathematicians. This was basically domestic nerd sniping.

For more thorough coverage, see Jacob Bourjaily’s scientists and mathematicians on money. You may also be interested in purchasing portraits of Gauss. Newton was on the one-pound note when there was such a thing; the Euler ten-Swiss-franc note is out of print. Bourjaily collects notes with scientists and mathematicians on them and has a list of what he’s looking for; perhaps you can help him out?

Weekly links for September 9

Samuel Arbesman on the mathematics of parked cars, referring to a 2007 paper by Petr Seba “Parking in the city: an example of limited resource sharing”. (This gets more fun when you live in a city where lots of people have garages, but there is also lots of street parking. San Francisco is an example.)

Aaron Clauset and Ryan Woodard, Estimating the historical and future probabilities of large terrorist events. Via physics arxiv blog.

Secrets of Alice in Wonderland, alternating between the reading of pieces of the Alice in Wonderland stories by Cobi Smith and explanations of the underlying mathematics by David Butler. If you like this sort of thing you might be interested in The Annotated Alice: The Definitive Edition, by Lewis Carroll and Martin Gardner.

The Weatherman Is Not a Moron is an excerpt from Nate Silver’s new book The Signal and the Noise: Why So Many Predictions Fail-but Some Don’t

Making Math Matter: Differential equations in action

Udacity’s “Making Math Matter: Differential Equations in Action” by Jörn Loviscach and Miriam Swords Kalk began its premiere run yesterday. See the trailer below:

You need to know a little programming (the course uses Python); it wouldn’t hurt to know a little calculus. This looks like it should be fun.

I’m looking for a job, in the SF Bay Area. See my linkedin profile.

Mental math: how to convert Celsius to Fahrenheit

A lot of people know the formula for converting Celsius to Fahrenheit: multiply by 1.8 and add 32. Unfortunately this is somewhat annoying for mental-arithmetic purposes, because 1.8 is somewhat unwieldy. A few people suggest the rule of doubling the Celsius temperature, then adding thirty:
here, here, here. This is exactly correct at 10 Celsius / 50 Fahrenheit, and is off by one Fahrenheit degree for each five Celsius degrees . For example, it converts -20 C to -10 F (should be -4 F) and 40 C to 110 F (should be 104 F). So for weather-conversion purposes this is actually quite good, as 50 is right around the center of the “typical” weather range of 0 to 100. (I’m showing my roots here.)

For culinary purposes, I’ve seen the suggestion of doubling the Celsius temperature to get the Fahrenheit temperature. Solving the equation 1.8C + 32 = 2C gives C = 160, and 160 Celsius = 320 Fahrenheit, which is a fairly typical oven temperature.

As it turns out, in order to convert Celsius to Fahrenheit I don’t actually do the whole multiplying by 1.8 trick. Instead, I know what multiples of 5 degrees Celsius are in Fahrenheit:

C	0	5	10	15	20	25	30	35	40
F	32	41	50	59	68	77	86	95	104

I didn’t consciously memorize these. I knew the pair (0, 32) like everyone does (it’s the freezing point of water); (20, 68) is pretty common as room temperature. To get the others, note that the Fahrenheit temperatures go in steps of 9.

So to convert Celsius to Fahrenheit: say it’s 37 degrees Celsius. That’s near 35, so the Fahrenheit temperature must be near 95. But how far? Well, it’s two degrees Celsius warmer, or about four degrees Fahrenheit warmer; figure 1 Celsius degree is 2 Fahrenheit degrees. So 37 Celsius is 95 + 4 = 99 Fahrenheit. The truth is 98.6, which isn’t body temperature anyway. (You know that the whole 98.6 body temperature is an overly precise conversion of 37 Celsius, right? If not, now you do.)

Or right at this moment it’s 18 degrees Celsius in San Francisco. 20 Celsius is 68 Fahrenheit; it’s two degrees Celsius cooler than that, or about four degrees Fahrenheit. So 18 Celsius = 68 – 4 = 64 Fahrenheit.

In general, to convert Celsius to Fahrenheit, the method is as follows:

first, take the closest Celsius temperature from the first row of the table. Get a rough conversion into Fahrenheit from the second row.
for each degree Celsius you are above or below this approximation, add or subtract two Fahrenheit degrees from your rough conversion

The second step contributes an error of (2 – 1.8) = 0.2 degrees Fahrenheit for each Celsius degree of error — but no matter the starting Celsius temperature, one of the table entries is within two degrees of it, so we get an error of at most 0.4 degrees. If we’re rounding to the nearest integer anyway, who cares?

A simpler version is to only use every other column of the table; then you may end up with errors of as much as a whole degree.

(I didn’t realize this was what I was doing until I realized a few days ago that I could do these conversions in my head, and found myself trying to explain what I was doing. It would be harder between 0 and 32 F, because Celsius and Fahrenheit have opposite signs there, but I live somewhere now where it never gets below freezing.)

I’m looking for a job, in the SF Bay Area. See my linkedin profile.