Today in license plates: PIB4159, seen on a Porsche driving south on Georgia 400 just north of I-285, when I was coming home from work.  Georgia license plates are three letters followed by four numbers by default, so this isn’t a vanity plate. At least I don’t think it is.  But a B does kind of look like a 3 and a 1 together… unfortunately in the wrong order to make this is a six-digit approximation of pi.

(If they’d let me, I’d get CAB1729.  People would just think it was a normal plate.). I’ve always thought that it’s not quite so impressive that Ramanujan noticed that 1729 is the sum of two cubes in two distinct ways – it’s 1000 + 729 or 1728 + 1, and both of those are easy to see by eye.

For more, you should read Knuth on mathematical vanity plates.

The hot hand is real.  Joseph Stromberg at Vox  reports on this working paper by Joshua Benjamin Miller and Adam Sanjurjo and the decades of related research.  I had thought that the reason the hot hand appeared to not exist might be that players take harder shots when they’ve made their previous shots, or that defenses pay extra attention when someone gets hot.  It turns out that this is partially true, but also tests in the classical papers are underpowered, which I learned from Jordan Ellenberg describing a paper by Kevin Korb and Michael Stillwell.

Big Data and Chess: What are the Predictive Point Values of Chess Pieces?, by Rasmus Bååth.

There are a “standard” set of values for chess pieces: pawn = 1, bishop = 3, knight = 3, rook = 5, queen = 9. How well do these check out? Given a chess position one can find the difference in the number of each type of piece between the two players and see who wins. It turns out (according to this analysis) that the standard analysis gets the relative value of the pieces (i. e. non-pawns) right but undervalues pawns; this may be because the games in the dataset used are between very strong players, and pawns may be more valuable in their games.

I’ve thought of doing this analysis myself, but just haven’t gotten around to it. The obvious extension would be to take into account context – are pawns further up the board worth more because they have a likelihood of being promoted? Do values change based on the stage of game?

Apparently students in the UK have been protesting against the following question on a GCSE math exam (see e. g. coverage at The Guardian):

There are n sweets in a bag. Six of the sweets are orange. The rest of the sweets are yellow. Hannah takes a random sweet from the bag. She eats the sweet. Hannah then takes at random another sweet from the bag. She eats the sweet. The probability that Hannah eats two orange sweets is 1/3. Show that n²-n-90=0.

The probability that the first sweet is orange is . Now there are five orange sweets left out of , so the probability that the second sweet is orange, assuming that the first one is, is . Therefore we need to solve . Multiplying it out gives

and we can easily rearrange to get . So 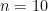; there are 10 sweets. (I guarantee you that a bunch of students went straight for the quadratic formula at this point – but you don’t have to, it’s easy to find two consecutive numbers that multiply to 90.) According to the BBC, setters of the exam point out that this was supposed to be one of the more difficult questions, “targeted at students aiming for A and A* grades”.

There’s a question this reminds me of, of which I don’t recall the original source: there are r raspberry sweets and b blueberry sweets in a bag. You take two of them at random; the probability that they have the same flavor is exactly 1/2. What are possible values for r and b? (Okay, so I’ve heard it with “red” and “blue”, but let’s go with fruit flavors.) (Okay, so I’ve heard it with “red” and “blue”, but let’s go with fruit flavors.) See for example this Quora question. This one is a bit trickier, and depends on getting lucky and choosing the right parametrization of the problem. If the number of reds/raspberries is and the number of blue(berries) is 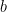, then we have

the first term is the probability of drawing red-red and the second is the probability of drawing blue-blue. We can rewrite as

but that isn’t much of a help, to be honest. Solving for in terms of 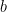gives

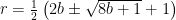
and if you happen to know the obscure piece of trivia that for integer 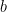, 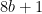is a perfect square if and only if 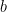is triangular, then you can show that and 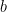must be two consecutive triangular numbers. For example leads to the solutions and .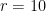

But if you use n = r + b, then is as pointed out at the Quora answer, 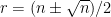(with different notation) and this doesn’t require knowing anything obscure. Setting leads immediately to the solutions , for example. In general, to make this work out the number of sweets needs to be a perfect square.

What if there are three colors of sweets? How can we choose the number of sweets of each color to make the probability of getting a match equal to one-third?

Do you like geometrical constructions? Then you should like the flag of Nepal, which is the only non-rectangular flag of a nation, is actually defined by a Euclidean ruler and compass construction in their constitution. See a step by step drawing of the construction or this video from Numberphile.

The flag of the state of Ohio is also non-rectangular, but sadly their laws only describe it as “burgee-shaped”.  It might be possible to extract a construction from the picture in this brochure from the Ohio secretary of state, but it looks like many of the points are specified but their position in a larger rectangle. Ohio’s flag is analytic geometry; Nepal’s is synthetic.