Tonight the God Plays Dice art department made blondies!
These are supposed to be made, according to the recipe, in a pan which is an eight-inch square. But we have no such thing. We do have a nine-inch circular pan, though. Will that do?
Well, what matters is that the two pans have the same area – and therefore that the same volume of batter will have the same thickness and cook roughly the same. (If you thought I was going to solve some PDEs and work out how the heat transfers, you haven’t been paying attention.)
A nine-inch circle has area  square inches, which is about 63.62. An eight-inch square, of course, has area 64 square inches. Not bad!
square inches, which is about 63.62. An eight-inch square, of course, has area 64 square inches. Not bad!
What would it take for this approximation to be exactly correct? This would require that  exactly; solving for
exactly; solving for  gives $\pi = 256/81″, which is often credited as an Egyptian approximation to
gives $\pi = 256/81″, which is often credited as an Egyptian approximation to  as it implicitly appears in the Rhind papyrus, an ancient Egyptian document of,problems in mathematics. In fact the setting in which this is established there is almost exactly this one – a circle of diameter 9 and a square of side 8 are said to have the same area. See for example these slides for a history of math class by Bill Cherowitzo.
as it implicitly appears in the Rhind papyrus, an ancient Egyptian document of,problems in mathematics. In fact the setting in which this is established there is almost exactly this one – a circle of diameter 9 and a square of side 8 are said to have the same area. See for example these slides for a history of math class by Bill Cherowitzo.
This isn’t the greatest approximation of  – in fact
– in fact 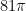 is about 254.46 – but it has the added “virtue” that 256 is a power of two, and 81 is a power of three. We could write
is about 254.46 – but it has the added “virtue” that 256 is a power of two, and 81 is a power of three. We could write 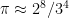 – it looks nicer that way, I think.
– it looks nicer that way, I think.
And because Internet law forbids me from mentioning food without posting a picture of it:

