Relatively Prime season 2

Samuel Hansen, the force behind Strongly Connected Components and other excellent mathematical podcasts, is releasing the second season of his longform series Relatively r Prime. The first episode, “The Lexicon”, focuses on the language (both words and symbolic) used in mathematics.

In this episode, Samuel revisits his old feud with Peter Rowlett on whether it’s “math” or “maths”. It turns out that, according to Google’s word2vec model (which RaRe technologies has a web tool for), math is to maths as sports is to sport.

Links for January 4

Evelyn Lamb on Shinichi Mochizuki’s proof of abc and Piper Harron’s thesis, and how they exemplify opposite ends of a continuum.

Alycia Zimmerman on teaching mathematics to schoolchildren with LEGO.

Andrew McKenzie lists nine paradoxes with a statistical theme.

The best charts of the year from FiveThirtyEight.

For the knitters out there, you can buy patterns to make mathematical objects from Woolly Thoughts. (I’m a bit sad I can’t buy the actual objects.)

Network visualizations of Shakespearean tragedies by Martin Grandjean.

The math-class paradox by Jo Boaler at the Atlantic.

Buy a 3-D printed digital sundial or hear how it works.

In blog posts that I don’t have to write becasue someone else did, Michael Quinn, Philip Keller, and Tyler Barron have all written solutions to FiveThirtyEight’s Riddler #2 (the one about geysers). The “official” solution by Brian Galebach (who proposed the problem) was published along with the next puzzle.

David R. Hagen figures out why the 11th in the month is mentioned less frequently than other days, answering a question from xkcd.

Alex Albright on the demographics of PhD students in the sciences.

Some properties of 2016

Happy 2016!

I noticed something a couple days ago – I’m 32 now, and it’s 2016, and 32 is a factor of 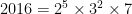$2016 = 2^5 \times 3^2 \times 7$ .

Last year, though, had the same property – 31 is a factor of 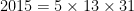$2015 = 5 \times 13 \times 31$ .

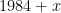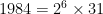So in which years will my age on New Year’s Day, $x$ divide the current year $1984 + x$ ? These are just the factors of $1984 = 2^6 \times 31$ .

(This seems like a nice problem – which numbers have two consecutive factors? But in fact that’s just a characterization of the even numbers.)

Some other properties of 2016:

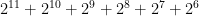
it has a nice binary representation as 11111100000; alternatively it’s the sum of consecutive powers of 2, $2^{11} + 2^{10} + 2^9 + 2^8 + 2^7 + 2^6$
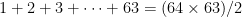
it’s a triangular number, $1 + 2 + 3 + \cdots + 63 = (64 \times 63)/2$
it’s the number of ways to arrange two same-color pawns on a chessboard, ${8^2 \choose 2}$
it’s divisible by every single-digit number except 5

2016 appears to be a relatively interesting number, appearing in 784 sequences in the OEIS – compare 179 sequences containing 2015 and 428 containing 2017. This is probably traceable to the fact that it has many prime factors – all of the above are essentially divisibility properties – and this is the big idea in the paper on “Sloane’s gap” by Nicolas Gauvrit, Jean-Paul Delahaye and Hector Zenil. (Don’t like reading? Check out the Numberphile video instead.)

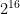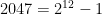In fact, back in 2009 Philippe Guglielmetti put together a spreadsheet giving the number of appearances in OEIS of each number up to $2^{16}$ , which you can download from this post (click on “feuille Excel”); at the time 2016 appeared in the OEIS more often than any other number between $1729 = 12^3 + 1$ and $2047 = 2^{12}-1$ inclusive.