Piper Harron wrote a thesis: “The Equidistribution of Lattice Shapes of Rings of Integers of Cubic, Quartic, and Quintic Number Fields: an Artist’s Rendering” which, in addition to proving an interesting result “laysplains” it along the way.

Sadly, “laysplain” doesn’t seem to be a word yet. Google it and you just find potato chips.

(via metafilter)

For those who are into this sort of thing: the problems from the 2015 Putnam exam are now available.

We’re buying a house today.

It turns out that although we’re moving about ten miles, both of our commutes stay about the same length. Both before and after the move, I’m going about 35 minutes and she’s going about 15.

Say my commute length is x and my wife’s commute length is y. You can imagine drawing a circle of radius x around my work and a circle of radius y around hers. (These are “circles” where the metric is driving time, not driving distance or distance as the crow flies.)  These circles intersect in two places, like circles do. (Bezout’s theorem says four, but two of those are at infinity, and there’s no way I’m living there.) We used to live at one of the intersections of these circles; we’re mvoing to the other one.

In the interest of security by obscurity, no map will be provided. Also, drawing a map with isochrones or with distances calculated along the road network isn’t really how I want to spend my morning.

It’s a good week for articles profiling mathematicians. Siobhan Roberts has written a fascinating profile of John Horton Conway at the Guardian, based on her biography of him, Genius At Play: The Curious Mind of John Horton Conway. And Gareth Cook has written The Singular Mind of Terry Tao for the New York Times. (Is that a math pun in the title?)

The Tao profile mentions the general (oral) exams at Princeton, and apparently Princeton math PhD students have an archive of student summaries of those exams; here is Tao’s.  (At Penn we had something similar although apparently no longer maintained. Such is inevitable for student-maintained resources like this, I suppose.)

C. Liam Brown has built a Battleship probability calculator, which (roughly speaking) works by finding the square which is the most likely to yield a hit given the set of hits and misses so far. You can play against it if you want. A lot of this might be said to be a web-friendly implementation Nick Berry’s analysis of the game, although analysis and implementation are two different beasts. (Funny, that keeps coming up in my day job…)

I’m a little late to this, but Igor Pak has a list of combinatorics videos (of lectures and seminars) and an explanation of why you should watch them, why you should let people make videos of you, and so on.

(Posting this because I happened to Google something unrelated, found a paper that Pak wrote that was useless to my actual purpose, but then remembered that I’d come across this months ago…)

Today in license plates: PIB4159, seen on a Porsche driving south on Georgia 400 just north of I-285, when I was coming home from work.  Georgia license plates are three letters followed by four numbers by default, so this isn’t a vanity plate. At least I don’t think it is.  But a B does kind of look like a 3 and a 1 together… unfortunately in the wrong order to make this is a six-digit approximation of pi.

(If they’d let me, I’d get CAB1729.  People would just think it was a normal plate.). I’ve always thought that it’s not quite so impressive that Ramanujan noticed that 1729 is the sum of two cubes in two distinct ways – it’s 1000 + 729 or 1728 + 1, and both of those are easy to see by eye.

For more, you should read Knuth on mathematical vanity plates.

The hot hand is real.  Joseph Stromberg at Vox  reports on this working paper by Joshua Benjamin Miller and Adam Sanjurjo and the decades of related research.  I had thought that the reason the hot hand appeared to not exist might be that players take harder shots when they’ve made their previous shots, or that defenses pay extra attention when someone gets hot.  It turns out that this is partially true, but also tests in the classical papers are underpowered, which I learned from Jordan Ellenberg describing a paper by Kevin Korb and Michael Stillwell.

Big Data and Chess: What are the Predictive Point Values of Chess Pieces?, by Rasmus Bååth.

There are a “standard” set of values for chess pieces: pawn = 1, bishop = 3, knight = 3, rook = 5, queen = 9. How well do these check out? Given a chess position one can find the difference in the number of each type of piece between the two players and see who wins. It turns out (according to this analysis) that the standard analysis gets the relative value of the pieces (i. e. non-pawns) right but undervalues pawns; this may be because the games in the dataset used are between very strong players, and pawns may be more valuable in their games.

I’ve thought of doing this analysis myself, but just haven’t gotten around to it. The obvious extension would be to take into account context – are pawns further up the board worth more because they have a likelihood of being promoted? Do values change based on the stage of game?

Apparently students in the UK have been protesting against the following question on a GCSE math exam (see e. g. coverage at The Guardian):

There are n sweets in a bag. Six of the sweets are orange. The rest of the sweets are yellow. Hannah takes a random sweet from the bag. She eats the sweet. Hannah then takes at random another sweet from the bag. She eats the sweet. The probability that Hannah eats two orange sweets is 1/3. Show that n²-n-90=0.

The probability that the first sweet is orange is . Now there are five orange sweets left out of , so the probability that the second sweet is orange, assuming that the first one is, is . Therefore we need to solve . Multiplying it out gives

and we can easily rearrange to get . So 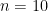; there are 10 sweets. (I guarantee you that a bunch of students went straight for the quadratic formula at this point – but you don’t have to, it’s easy to find two consecutive numbers that multiply to 90.) According to the BBC, setters of the exam point out that this was supposed to be one of the more difficult questions, “targeted at students aiming for A and A* grades”.

There’s a question this reminds me of, of which I don’t recall the original source: there are r raspberry sweets and b blueberry sweets in a bag. You take two of them at random; the probability that they have the same flavor is exactly 1/2. What are possible values for r and b? (Okay, so I’ve heard it with “red” and “blue”, but let’s go with fruit flavors.) (Okay, so I’ve heard it with “red” and “blue”, but let’s go with fruit flavors.) See for example this Quora question. This one is a bit trickier, and depends on getting lucky and choosing the right parametrization of the problem. If the number of reds/raspberries is and the number of blue(berries) is 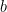, then we have

the first term is the probability of drawing red-red and the second is the probability of drawing blue-blue. We can rewrite as

but that isn’t much of a help, to be honest. Solving for in terms of 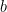gives

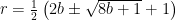
and if you happen to know the obscure piece of trivia that for integer 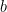, 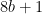is a perfect square if and only if 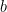is triangular, then you can show that and 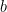must be two consecutive triangular numbers. For example leads to the solutions and .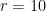

But if you use n = r + b, then is as pointed out at the Quora answer, 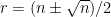(with different notation) and this doesn’t require knowing anything obscure. Setting leads immediately to the solutions , for example. In general, to make this work out the number of sweets needs to be a perfect square.

What if there are three colors of sweets? How can we choose the number of sweets of each color to make the probability of getting a match equal to one-third?