Erica Klarreich at Quanta on large prime gaps.

What makes Paris look like Paris?

Math-inspired Christmas ornaments (sadly, I don’t have a tree).

Nathan Yau at FlowingData has a list of data-ish physical gift things.

From the archives of the MAA, video of David Blackwell on predicting at random (1966).

Not only is my age prime, but it’s a Mersenne prime! Barring some great advances in medical technology it’s the last time I’ll be able to say that.

(What else is interesting about the number 31? It seems like a pretty nondescript age life-wise, so I was hoping for some interesting math at least.)

Brainfilling Curves: A fractal bestiary by Jeffrey Ventrella.

Matt Parker on Numberphile on Stern-Brocot numbers, fractions, and rational numbers (an exposition of my favorite elementary paper, Recounting the rationals by Neil Calkin and Herbert Wilf)

From DataLab (FiveThirtyEight): how common is it for a man to be shorter than his partner? (Mona Chalabi) and which city has the most predictable weather? (Nate Silver and Reuben Fischer-Baum.

I’m just finding this now, although it’s a few months old: there’s a moving sculpture at a biotech firm in Cambridge, Mass. that can look like just a bunch of balls suspended in space until you look at it from the right angle and at the right time.

How to wrap a gift using the least paper.

A puzzle on escaping from prison using coins and a chessboard from DataGenetics.

Brian Hayes (bit-player) onFour Fifths = A Fifth and the Euler-Fermat conjecture.

A video from Numberphile on Sloane’s gap and the paper it’s based on.

How game theory helped improve New York City’s high school application process. (It’s basically the Gale-Shapley algorithm.)

Mike Lawler has a single post assembling the lectures (by Terence Tao, Jacob Lurie, Richard Taylor, Simon Donaldson, and Maxim Kontsevich) from the Breakthrough Prize symposium in mathematics. Here are the abstracts.

Stephen Pettigrew at FiveThirtyEight writes about the 2014 elections that ended in a tie. These are generally resolved by games of chance. The elections that are mentioned there are small ones (two city councilors and a county commissioner); is this because most elections are small or because small elections are more likely to end in ties? Some of both, I think.

Empirically, according to this paper by Casey Mulligan and Charles Hunter, in the period 1898-1992, six out of 16,577 elections to the US House of Representatives were decided by ten votes or less (one was exactly tied), while nine out of 40,036 elections to state legislatures were decided by one vote or less (and two were exactly tied). Looking at this suggests that state elections are more likely to be tied – perhaps because they’re smaller. And in fact the probability of having a “pivotal” election (an election that could be changed with a single vote, according to Mulligan and Hunter, appears to vary like 1 over the number of votes.

This is easy to explain. Very roughly speaking, if we look at two-party elections (I’ll follow Brian Hayes and call the two parties Red and Blue), the proportion of the vote that Blue receives has some distribution; for the sake of argument let’s say that it’s uniform on [0.25, 0.75]. (I don’t actually expect that it’s uniform, but the value at 0.5 is what matters.) Then for Blue’s proportion of the vote received to be in [0.5 – 0.5/n, 0.5 + 0.5/n] in an n-vote election (if n is even, which is the only case when a tie can actually happen) has probability 2/n. The constant 2 depends on my assumption of a prior distribution (although it turns out to match up well with the empirical data) but the 1/n dependence does not. Mulligan and Hunter go a bit deeper and suggest a two-tiered model (there’s a prior on the true proportion of Blue voters, and then voters vote at random according to this) but the broad conclusion is the same.

This suggests that models like the Banzhaf power index don’t make sense in measuring voting power, since votes are not coin flips. The paper The Mathematics and Statistics of
Voting Power by Gelman, Katz, and Tuerlinckx suggets some more realistic models than the coin-flip model.

Incidentally, before looking at the Mulligan and Hunter paper, I was actually thinking that the probability of a tied election would go like the -3/4 power of the number of voters. My thinking was as follows: I had an argument like the 1/n one in my head, but the probability of getting n/2 heads in n coin flips goes like n^-1/2, so why not pick something in between?

And once we’ve found ties, how do we break them? In the three ties mentioned by Pettigrew, one was broken by picking a name from a hat, one by picking blocks from a bag, and one (for a seat on the Neptune Beach, Florida city council) by the following baroque procedure:

Rory Diamond and Richard Arthur had each received 1,448 votes for Seat 4 on the Neptune Beach City Council. To break the tie, Diamond’s name was drawn from a bag by a third party. This allowed Diamond the chance to call the coin toss. He won the toss by calling heads. Because of this, he could decide whether to draw first or second from a bag of ping-pong balls, numbered one through 20. He deferred to Arthur, who drew No. 12. The ball was replaced, and Diamond then drew No. 4. Arthur won the seat.

Why three rounds? Does this provide more randomness than just one round? This Florida Times-Union article suggests that Supervisor of Elections Jerry Holland “wanted the results to seem as random as possible.”

Today PNC Wealth Management announced its Christmas Price Index. This is the cost of buying all the gifts in the song The Twelve Days of Christmas. All 364 of them.

Where’d that number come from? Well, there is one on the first day: a partridge in a pear tree. There are three gifts on the second day: two turtle doves, and a partridge in a pear tree. And so on up until 78 gifts on the twelfth day: twelve drummers drumming, eleven pipers piping, and all the way on down. The total number of gifts bought is 1 + 3 + 6 + … + 78 = 364, which is, coincidentally, one less than the number of days in the year. (The number 365, being just the nearest integer to a ratio of two times, can’t have any number-theoretic significance.)

But what if Christmas lasted n days instead of three? What then?

The identity is a special case of

$

which in turn is a special case of the “hockey-stick identity”

$

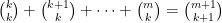or in more compact notation

.

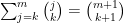Let’s prove this identity. We want to choose 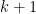elements from the set . We can do this by first choosing the largest element, and then choosing the $k$ smaller elements. If we choose to be the largest element, there will be ways to pick the smaller elements from ; summing over the possible values of gives the answer.

But a different way of counting is suggested by observing that over the 364 days, the true love receives:

• partridges-in-pair-trees;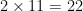
• turtle doves;
• french hens;
• …
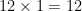• drummers drumming

and so we get the identity

.

If there’s anything right with the world, this ought to be a special case of

and why should this be? Let’s write this as

where the reason for the somewhat strange indexing will be apparent shortly.

Let’s count subsets of the set of size 3. We can write each such subset as where we require . > Then we’ll count these subsets according to the difference . To construct such a set with we must:

• choose . must be between and inclusive, so there are possible choices.
• choose 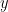. 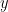must be between and 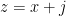exclusive, so there are 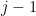possible choices.

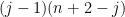At this point is fixed. So there are ways to choose the 3-set with ; summing over the possible values of gives the answer.

(Is there a natural generaliztion of this later identity that counts sets of sizes 4 or larger?)

So by counting sets of size 3 in two different ways, we’ve made combinatorial proofs of two different identities, both with a binomial coefficient with “lower number” 3.

The 364-gift total has been observed in various places; people who have looked at the math instead of just adding up the numbers include Murray Bourne and Brent Yorgey. And Knuth observed that the song itself has a space complexity of .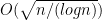

Stian Haklev on Starting data analysis/wrangling with R: Things I wish I’d been told.

Zulko on Things you can do with Python and POV-Ray (a raytracing engine).

Sanjoy Mahajan has a new book out, The Art of Insight in Science and Engineering” Mastering Complexity. This looks like it could be thought of a more science- or engineering-themed sequel to his Street-Fighting Mathematics.

Nigel Stanford’s Cymatics “is the science of visualizing audio frequencies.”

Does teaching gamblers about probability make them less likely to gamble? (Yes.)

FiveThirtyEight has a nerd holiday gift guide.

From Katie Steckles at the Aperiodical, Twitter’s favorite fictional mathematicians.

From A. O. Scott’s review of The Imitation Game, the new Alan Turing biopic:

“The Imitation Game” is rated PG-13 (Parents strongly cautioned). Illicit sex, cataclysmic violence and advanced math, most of it mentioned rather than shown.

First, advanced math is reason for caution? Um, no.

Second, what’s the difference between “mentioning” and “showing” mathematics anyway? This seems to be connected to the philosophical use-mention distinction, Godel numbering, and so on, but I doubt that Scott is trying to make a metamathematical point. This may just mean that people in the movie don’t sit around scribbling on pieces of paper but rather talk about the fact that they have done so, which is good, because I’ve watched people do math and there’s really nothing to see.

In honor of Thanksgiving: take a look at Niall MacKay’s paper Of bombs and boats and mice and men: a random tour through some scaling laws.

I mention this because one of the scaling laws there is the time it takes to roast a turkey – you can work out from dimensional analysis that roasting time is proportional to the two-thirds power of mass. Specifically, the thermal diffusivity κ of meat (or any other substance) – that’s the constant in the heat equation – has dimensions of length squared over time. Since the only relevant parameter is the length of the turkey l, roasting time must be proportional to l²/κ. But assuming a spherical turkey, length is proportional to the cube root of mass, giving the two-thirds law.

Happy Thanksgiving! And for my readers abroad, happy Thursday.

Mona Chalabi and Andrew Flowers figure out the most common name in America, using some data by Lee Hartman to correct for the fact that first name and last name are not independent, but tend to cluster based on ethnicity. A fun fact: apparently people avoid alliteration. Does this extend to martial name-changing? For example, say my wife’s first name starts with an L, as does my last name; does that make her less likely to have changed her name upon marriage? She didn’t, but I can’t attribute that to the alliteration.

From Jawbone via the Atlantic, people don’t exercise when it’s cold. (A bit less obvious in the data is that they don’t exercise when it’s hot, either.)

David Mimno at Cornell has a fun word similarity tool based on a corpus of pre-1923 books.

Michael Harris at Slate writes about the Breakthrough Prize, which are trying to be the “Oscars of science”. He’s got a book coming out called Mathematics Without Apologies, which is at least the second in a line of titles riffing on A Mathematician’s Apology, after The Unapologetic Mathematician. (And don’t forget Second-Rate Minds (expositors, according to Hardy).

Tim Hersterberg at Google has written on What Teachers Should Know about the Bootstrap: Resampling in the Undergraduate Statistics Curriculum

From Todd W. Schneider (who’s on fire lately): the Reddit front page is not a meritocracy. (Disclaimer: Schneider, or someone with his same name and similar demographic history, was a year behind me in high school.)

Christian Perfect linked to a short documentary, Logically Policed by Damiano Petrucci, about mathematicians.

Rob Hyndman on visualization of probabilistic forecasts.

Mark Jason Dominus on teaching his daughter algebra.

Emilia Petrisor writes (with code – an iPython notebook) on domain coloring as a way of visualizing complex-valued functions

Mike of mikemathspage and his kids made some videos on the Collatz conjecture and a variation on it due to Conway. (The Conway variation is in his paper “On Unsettleable Arithmetic Problems”.)

From Pip ( = Dick Lipton + Ken Regan) at Gödel’s Lost Letter and P = NP: two vs. three. Why is two so special?

Rasmus Bååth and Christian Robert wrote a A Brief Review of All Comic Books Teaching Statistics in Chance.

There’s a second edition of Skiena’s Algorithm Design Manual.

Last Friday morning (the 14th) it was unseasonably cold in Atlanta. On the way to work I noticed my car’s display giving the following temperature readings: 28, 30, 32, 34, 36 – all in Fahrenheit. It somehow knew to avoid the odd numbers.

But in the evening of the same day it read 39, 41, and 43. Now it knew how to avoid the even numbers.

I watched a little more closely for a while – on a trip on Sunday morning it read 46, and then 48. On Monday morning, 50, 52, and 54. Even again.

A puzzle for readers: what’s going on? (I know the answer.)