Stephen Wolfram (Mathematica, A New Kind of Science, Wolfram Alpha) is doing an AMA at Reddit. (That stands for “ask me anything”; it’s what it sounds like.) His username there is “StephenWolfram-Real”; it’s probably best to just search for that and not wade through the comments.

Some interesting points:

• it’s a big challenge to let people know what’s available. I’ve run into this, even just using it for mathematical stuff, although this is mostly because I don’t know Mathematica syntax.
• Wolfram believes that W|A will invent more things on the fly ten years from now. That certainly seems like what you’d get out of an increase in computing power.
• a big difficulty in going from developing Mathematica to developing W|A is that W|A uses a lot more heuristics.

Probably every couple years I have occasion to tell people “hey, did you know there’s some guy that tried to get the worst possible score on the SAT, on purpose?”

Well, there is. His name is Colin Fahey, and he writes about his experience on his web site. However, since last I looked at his web page he’s added some material on the mathematics of the SAT (multiple-choice guessing and the like, not the mathematics tested ON the SAT) and some, um, comedy.

Did you know:

1. the SAT has a “variable” section, which is not part of the student’s score but is used for research purposes. Section 5.6 of this document analyzes whether you can determine which section is the variable section during the exam; I’m reminded of what Wikipedia calls the unexpected hanging paradox (and what I call the “pop quiz paradox”, because I teach, although I’m not the sort of teacher who gives pop quizzes). I remember reading in SAT prep books that “you shouldn’t try to guess which section is the experimental section during the test”; I wonder if anybody actually goes to that trouble.

2. those “fill-in-the-blank” questions are really “12700-choice” (section 8)? What sort of person would work that out? (Okay, so I would have worked that out if someone else hadn’t already.) There are 22308 possible answers, but some of them (like 3..0) don’t code for actual numbers, and others are equivalent (like 1/4_ and 0.25, where _ denotes a blank).

3. the distribution of the answers to said fill-in-the-blank questions (section 11.3) does not appear to be some nice, well-known distribution? This is true of exam questions in general, I think; answers tend to be close to unity. I gave an exam a few days ago where I asked students to compute the correlation coefficient of a small data set. The correlation was obviously negative, but the data did not fall on a straight line; the “simplest” guess, -1/2, would have been right.

4. Section 12.2 features a plot entitled “rough interpretation of the .52 correlation coefficient between the SAT combined scaled scores and college freshman GPA” (by the College Board); they seem to assume that SAT is a linear function of GPA plus a uniformly distributed error. Um, what? I’m not saying that the errors should be normal — I haven’t actually seen the data but I’m guessing there’s some compression at the high end of the GPA scale — but that’s at least a little more realistic.

Why do introductory real analysis courses teach bottom up?, from math stack exchange.

Comments by Tim Gowers and Izabella Laba on the Elsevier boycott.

On the distribution of time-to-proof of mathematical conjectures, paper by Ryohei Hisano and Didier Sornette.

The Diagram Prize shortlist is revealed; this is the prize for oddest book title of the year. No math books this year, unlike 2010 winner Crocheting Adventures in Hyperbolic Planes and 2009 nominee The Large Sieve and its Applications. (via Marginal Revolution)

Stefan Collini, The threat to our universities, from the Guardian (so it’s about British universities, but probably applies on both sides of the Atlantic).

David Smith of Revolution Analytics on The Uncanny Valley of Big Data, on how predictive technologies are getting good enough to creep people out; see that New York Times article from a couple weeks ago.

Bret Victor looks for a better interface for mathematics, via Hacker News.

Robert Lucky asks is math still relevant (for engineers).

Jordan Ellenberg has a heart-shaped plot of the American electorate obtained by principal component analysis of some raw polling data.

Why the progress bar is lying to you.

A periodic table of visualization methods which at least tries to keep similar methods near each other like the actual periodic table does, and acompilation of infographic resources.

On NPR’s weekend edition, Alexander Masters talks about his book Simon: The Genius in my Basement, a biography of his landlord, the group theorist Simon Norton.

Keith Devlin at Devlin’s Angle on the difference between teaching and instruction. On my more frustrated days as a teacher I find myself saying that what I’m doing is not teaching; Devlin argues that what we do in front of large groups, getting them to know how to solve specific types of problem, is better called “instruction”. He reserves “teaching” for a more interactive process, which is perhaps what I meant as well. (I do find what I do in office hours, working one-on-one with students, to be “teaching”, but my friends will all tell you that I lament that nobody comes to my office hours this semester.)

The gathering of math geeks who are taking over sports, an article on this weekend’s MIT Sloan Sports Analytics Conference. I wonder if I would have mocked this back when I was an undergrad at MIT. Sloan is the business school, and I hung out in decidedly anti-business-school crowds; on the other hand, sports statistics are fun. (Why haven’t I posted about them, you ask? Because I’m mostly a baseball fan, and it’s not baseball season.)

Kevin Lynch and the imageable Boston, from Bostonography.

A profile of Patrick Ball, “human rights statistician”. This New York Times piece from 2008 suggests what sounds like a capture-recapture approach to estimate the true number of crimes committed — if you have two lists of murders with little overlap, there are probably many you haven’t seen, but if your two lists have a lot of overlap you can bet they’re close to complete. (Via simply statistics.)

The manual of mathematical magic.

Calvin and Hobbes math jokes.

Becoming an expert statistician, by Ann Maria de Mars.

Readings for an honors liberal art math course, reader suggestions at MathOverflow.

Major League Baseball has adopted a new playoff format. Each of the National and American leagues is divided into three divisions. This won’t change, but five teams from each league will make it to the postseason: the three division winners, and two wild cards, the best two teams among the non-division-winners. The two wild cards in each league will play in a one game playoff;. Then there are four teams left. The wild card will play the division winner with the best record, and the two remaining division winners will play each other, in a best-of-five series; the winners of those two series play best-of-seven in the League Championship Series; the winner moves on to the World Series.

mlb.com indulges in a little how would history be different with the new playoff format, mostly to draw the eyeballs of fans of, say, the 2005 and 2006 Phillies. (Readers of this blog’s former incarnation will know I’m a Phillies fan, in exile now in the Bay Area, which made 2010 hard.) In a fourteen-team or sixteen-team league it’s not surprising that there are a lot of teams that just barely miss the playoffs; the difference between the fourth-best and fifth-best team is likely to be pretty small. (The difference between the fifth-best and sixth-best team is probably even smaller on average, being closer to the middle of the distribution.)

The natural question from a probabilistic/statistical point of view, I think, is “what’s the probability that the best team wins the World Series”? As you add more layers of playoffs, this seems like it would go down. But on the other hand, this wrinkle seems like it might push up the probability of the best team winning the World Series. The best team is likely to have the best record in its league (“be the first seed”). This previously would have meant they faced the wild card team in the first round. Now the first seed’s first-round opponent is actually slightly worse than previous, on average. They face a team picked essentially by a coin flip between the fourth seed (the former wild card, i. e. the best non-division winner) and the fifth seed (the second best non-division winner), and that team will have likely used its best pitcher in the play-in game.

So somewhat paradoxically it seems that this helps the very best teams, at the expense of those slightly-above-average teams that somehow manage to slip in. However this argument seems handwavy enough that I don’t know for sure. One thing to do would be to look at old data, but I suspect the effects are fairly small and hard to see in MLB’s hundred-year data set. The new system is suppoedly based on simulations but I’m not sure what that means; I may just have to do my own simulation to be sure.

I recently read Magical Mathematics, by Persi Diaconis and Ron Graham. I am not a magician, so I’m not really qualified to comment on the magic. But these are two first-rate mathematicians and there are some nice little bits of mathematics in here. Here’s one of them.

At one point (pp. 124-125) they discuss the I Ching. Diviniation from this book requires constructing, essentially, a sequence of six bits; this enables one to pick out one of 2⁶, or 64, “hexagrams”. Each hexagram has some associated text; that text is supposed to be interpreted as a commentary on the answer. (How far we have fallen! Now we have the magic 8-ball. And, I suppose, fortune cookies.) It’s traditional to represent each bit by either a broken line or a solid line, and furthermore to call those lines “changing” or “unchanging” — so there are really four possibilities:

• broken changes to solid (associated with the number 6)
• solid stays solid (associated with the number 7)
• broken stays broken (associated with the number 8)
• solid changes to broken (associated with the number 9

What is wanted is a way to pick one of these four possibilities at random.

One classical method for generating a random hexagram works as follows: begin with 49 sticks. Divide them into two piles at random. Set one stick aside; divide the remaining sticks into two piles. From each pile, count off the sticks in groups of four; add the last (possibly incomplete) group the one stick that was set aside.

You end up with a pile of either five or nine sticks — the two large piles had forty-eight sticks, and the groups other than the last contain some multiple of four. So the two last piles together contain a multiple of four sticks, either four or eight.

You now have either forty or forty-four sticks; repeat the whole procedure, setting one aside and breaking up into groups. You’ll end up with either four or eight sticks. Remove these, and repeat again; you’ll get a pile of either four or eight sticks.

So you have three small piles: one containing five or nine sticks, two each containing four or eight. Call a pile of size eight or nine “large”, and a pile of size four or five “small”; for each small pile score 3, for each large pile score 2. The sum of these three scores is 6, 7, 8, or 9, which gives the desired two bits.

There are other methods, often based on flipping coins; many of the more modern ones are criticized for not having the same probability distribution as this “classical” method. It’s not hard to come up with a method that gives half broken and half solid; but getting the “right” frequency of changing lines of each type is trickier.

Surprisingly, Diaconis and Graham just give the probabilities of getting 6, 7, 8, or 9, but don’t show how to compute them. (I say this is “surprising” because there seemed to be an indication that these probabilities would be given at the end of the chapter. So I want to briefly indicate how they’d be computed.

Let’s consider the first splitting. We take a pile of 48 and split it into a left-hand pile and a right-hand pile. The left-hand pile, we assume, is equally likely to have a number of sticks of the form or , leaving 1, 2, 3, or 4 sticks to be set aside respectively. In these cases the right-hand pile will have 3, 2, 1, or 4 sticks. So one-fourth of the time we set aside a large pile, and the rest of the time we get a small pile.

In each of the second and third splittings we start with a number of sticks which is a multiple of four; remove one stick; then go through the splitting process. Here, if the left-hand pile has 1, 2, 3, or 4 sticks in its final group then the right-hand pile will have 2, 1, 4, or 3 sticks in its final group; no matter what happens we must end up with three more than a multiple of four. So half the time we set aside a large pile, and half the time we set aside a small pile.

So we get a small pile on the first splitting with probability , and on each of the later splittings with probability .     The probability that there are three small piles is ; that there are two small piles is 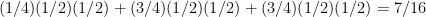; that there is one small pile is ; and that there is no small pile is .

The interesting thing to me is that if you only care about the parity of the number of small piles — that is, the initial broken-solid distinction — then there’s a lot of “extra” randomness here.  You could just take the results of a single splitting, starting with a pile with size a multiple of four, and use that to get a bit which is equally likely to be broken or solid. In fact if we flip any number of (independent!) possibly biased coins, as long as there is at least one fair coin we’re equally likely to get an odd number or an even number of heads. But psychologically, perhaps people want to see multiple steps in the process – it gives the sense that the result is somehow “more random”.

Rick Wicklin asks: which initials are most common?
This is followed with a simulation of the birthday problem. There are 676 different pairs of initials, so you might expect that to have probability 1/2 of two people in a group having the same initials, you’d need 31 people. This is the smallest for which , the probability that people have different initials if all initials are chosen independently and uniformly at random, is less than one half. From the simulation, though, we see that it only takes 18.

A question that Wicklin doesn’t try to answer, though, is whether first and last initials are independent. In Wicklin’s data set of 4,502 employees at SAS (where he works), 403 people have first name starting with M, and 224 people have last name starting with L. 14 have the initials ML. From those marginal frequencies you’d expect ; apparently in this sample parents with L last names are somewhat less likely to give their children M first names than in the population at large, although the effect is not statistically significant. (Spare me the usual data-mining caveats. ML is chosen not for any special properties it may have, but because they are my initials. If you looked at the data you know you started with your initials.)


inits = read.csv("C:/Users/Michael/Desktop/blog/initials.csv")
inits = inits[with(inits,order(I1,I2)),]
x=matrix(inits$COUNT,26,26,T)


A chi-squared test for independence (chisq.test(x)) gives with 625 degrees of freedom, and R reports but warns that “chi-squared approximation may be incorrect”. Some of the cell counts are quite small (in fact, zero is common!), which is the reason. So we resort to Monte Carlo methods. The call

chisq.test(x, simulate.p.value=T, B=10^6)

simulates a million contingency tables with the distributions of first and last initials given in Wicklin’s data — assuming those are independent — and reports the proportion of those tables which have χ² larger than 915.4.

When I ran this simulation I got p = 0.005138, still significant but much less extreme than the former results. And as Wicklin points out, SAS is ethnically heterogeneous; it might be that in homogeneous populations first and last initials are independent, and dependence comes from aggregation. For an extreme example, say that there are two kinds of people, red and blue; red people’s first and last initials are independent and uniformly distributed over the first half of the alphabet, and blue people’s over the second half. But I don’t have a big ethnically homogeneous data set to test that on.