Here’s some bad math: The Marketing Robot says that it’s the US that’s most excited about the royal baby, because we used the #RoyalBaby hashtag the most.

But the US (997,077 tweets) only beats the UK (344,806) by a ratio of 3 to 1… and we have five times as many people as the UK.  So per capita, the UK posted more, as befits the fact that this is a UK story.

Also, France has 320,021 tweets to the UK’s 344,806, and 65 million people to the UK’s 63 million. So France has nearly the same number of #RoyalBaby tweets per capita as the UK. But Frenchmen are like mathematicians, in that they don’t speak English. Perhaps French people care more about the royal baby than British people?

And Canada only had 37,272 tweets – 1/27 of the US total, despite having 1/10 the population. The British monarch is the head of state of Canada. And as you might remember, the US fought a war over that issue. Does Canada care less about its future head of state than the US?

The Irish Times reports on the Wranglers of Cambridge University

Jack Moore writes at Baseball Prospectus on The Secret History of Sabermetrics. I found F. C. Lane’s 1916 article Why the System of Batting Averages Should Be Changed, linked to there, quite interesting.

Nate Silver reviews a pair of children’s books on Paul Erdos for the New York Times, which he’s leaving for ESPN, returning to his sports roots. Josh Levin at Slate has eight sports questions for Silver.

David Eppstein’s Wikipedia user page has a compendium of “did you know?”s about things mathematical. I also learned from Eppstein’s blog about a talk that Erik Demaine gave about how and why he does his research.

From Cats in Drag, coloring Pascal’s triangle by residues mod n.

Jason Davies asks can you hear the shape of a drum graph.

Erica Klarreich, writing for Quanta, explains the work of Manjul Bhargava and Arul Shankar towards solving the minimalist conjecture regarding rational points on elliptic curves.

David Radcliffe asks about a generalization of the birthday problem.

Gerard Butters, Frederick Henle, James Henle, and Colleen McGaughley on Creating Clueless Puzzles (a Sudoku variant).

Robin Houston animates turning a triangle into a square (following Dudeney).
Roderick Little recently published in the Journal of the American Statistical Assocation In Praise of Simplicity not Mathematistry! Ten Simple Powerful Ideas for the Statistical Scientist.

Vienna Teng has written the hymn of Acxiom.

Jeremy Kun explains Bezier curves.

Over at MathOverflow, how does the work of a pure mathematician impact society?

Nautilus magazine on optimization gone too far: Unhappy truckers and other algorithmic problems

Tom Tango, while writing about lineup construction in baseball, pointed out that batters batting closer to the top of the batting order have a greater chance of setting records that are based on counting something – for example, Chris Davis’ chase for 62 home runs. (It’s interesting that enough people see Roger Maris’ 61 as the “real” record that 62 is a big deal.) He observes that over a 162-game season, each slot further down in the batting order (of 9) means 18 fewer plate appearances.

Implicitly this means that every slot in the batting order is equally likely to end the game — that is, that the number of plate appearances for a team in a game, mod 9, is uniformly distributed over {0, 1, …, 8}.

Can we check this? There are two ways to check it:

• 1. find the number of plate appearances in every game. This is boring.
• 2. come up with a model for the number of plate appearances in a game and see what comes out. This is exciting.

We need some basic statistics. From baseball-reference.com’s 2012 MLB season page on batting, we can find out that last year there were 184,179 plate appearances. From the season pitching page we learn there were 43,355 and a third innings pitched; at three outs per inning that’s 130,066 outs. So 70.6% of plate appearances include an out; 29.4% don’t. (I’m simplifying here in not accounting for double or triple plays, which come on plate appearances with more than one out.)

The question then boils down to: how many plate appearances does it take to get 27 outs? (Again, I’m simplifying: sometimes the home team doesn’t bat in the bottom of the ninth, there are extra innings, about which you should read this paper by Darren Glass and Philip Lowry, and so on.) That’s given by one parameterization of the negative binomial distribution. Let’s have the following model of baseball:

• The game consists of a series of plate appearances.
• Assume that any plate appearance has probability 1-p = 0.294 of no outs, and p = 0.706 of one out.
• When you get 27 outs, the game is over.
• Nobody keeps score. This isn’t real baseball.

Then what’s the probability that the game ends on the nth plate appearance, for any 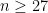? Among the first n – 1 plate appearances there must be exactly 26 outs; the probability of this happening is . Then the last plate appearance must be an out, which happens with probability p. So the probability of this game ending in plate appearances is
.
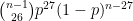(Incidentally, if we set we get this model’s estimated probability of a perfect game. It’s (0.706)²⁷, which is about one per 12,000 team-games. There have been 21 perfect games since 1900 and about 360,000 total team-games since 1900, for one in 17,000 or so – roughly in the right neighborhood, at least, for such a crude model.)

It turns out that a baseball game is not quite long enough to get the distribution to totally equalize. Here’s a plot of the distribution of the number of plate appearances per game:

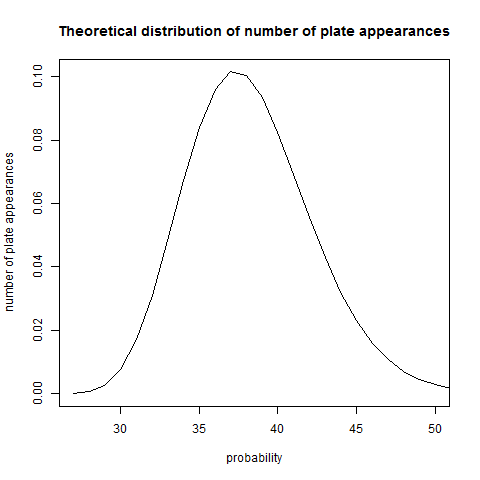
The distribution is not incredibly wide – the standard deivation is 3.99. Is this wide enough to get uniformity mod 9? Not quite. In the plot below, the red, green, and blue lines represent the probability of the game ending in the fourth, fifth, and sixth times through the order (28-36, 37-45, and 46-54 plate appearances, respectively), with the batter in the slot indicated on the x axis. The black line is the overall probability of ending on a given slot – the sum of the red, green, and blue lines, plus some other lines that are suppressed (games with 27 plate appearances, or 54 or more) that are graphically indistinguishable from zero.

The probability of the game ending with a batter in the kth slot in the order is given by the table below:

slot number	1	2	3	4	5	6	7	8	9
prrobability	.118	.114	.108	.104	.103	.106	.111	.116	.120

So the distribution is visibly not flat – but flat enough for Tango’s practical insight to make sense. Maybe moving someone up is expected to get them 17 extra plate appearances, or 19, instead of 18, depending on the slot. But the point still stands.  In practice the distribution of the final slot is probably even flatter than it appears here – the distribution of the number of plate appearances should be wider, since teams differ in skill, there are extra-inning games or games in which the home team doesn’t bat in the ninth, and so on.

Here’s a ten-minute video featuing Hannah Fry of UCL on the London riots of two summers ago. She’s a mathematician, and talks about the mathematics useful for understanding riots:
– the geography of rioting being like the geography of shopping – so certain parts of the city are more susceptible to rioting than others
– predator-prey interactions can br used to model the interaction between police and rioters
– the spread of the idea to riot is like the spread of an epidemic, and susceptibility to rioting seems to be connected to recent cuts in social services.

The original paper being described in this video is in Nature. I learned about it from FlowingData.

Greg Van Niel caught four foul balls at Sunday’s Cleveland Indians game.

ESPN reported that this is a one-in-a-trillion event – a number due to Ideal Seat, which I’ll take to mean that this guy had a one-in-a-trillion chance of catching four fouls. This is immediately suspicious to me. Total MLB attendance last year was about 75 million, so a one in a trillion event should happen once every thirteen thousand years. The fact that it happened, given that we’ve had way less than thirteen thousand years of baseball, is evidence that this computation was done incorrectly.

Somewhat surprisingly, given how small the number is, it actually seems to be an overestimate. I’ll assume that their numbers are correct: 30 balls enter the stands in an average game, and there are 30,000 fans at that game. Say I’m one of those fans. Let’s assume that all foul balls are hit independently, and that they’re equally likely to be caught by any person in the stands. The probability that exactly four balls will be hit to me are , where . This is about , or one in thirty trillion. (The probably that five or more balls will be hit to me is orders of magnitude lower than that.)

IdealSeat also claims that two fans caught two foul balls in the same game last year. I suspect that there’s some massive underreporting going on here, because the same analysis gives that the probability that I’ll get two balls is , which is about one in two million. So this should have happened 35 to 40 times last year – it’s just that most of the people who it happened to didn’t bother telling anybody! (Other than their friends, who probably didn’t believe them.)

What’s wrong with the one in a trillion, or one in thirty trillion, numbers?

• They assume that all foul balls are uniformly distributed over all the seats. This is patently untrue. Some seats by definition can’t receive a foul ball, because they’re in fair territory. Some seats, although they can theoretically receive a foul ball, just won’t. Ideal Seat has a heatmap of foul ball locations at Safeco Field in Seattle — basically the closer you are to home plate, the better your chances. Your chances of getting a foul ball drop off much faster with height than with horizontal distance. In addition, aisle seats are more likely to be the closest seat to where a ball lands than adjacent non-aisle seats.
• They assume that all foul ball locations are independent. I don’t know if there’s data on this, but batters have tendencies on where they hit balls in play; they should have tendencies on where they hit foul balls as well.
• They assume that a person can only get foul balls hit to their seat. This might be true in, say, San Francisco (where most games sell out), but it’s not true in Oakland (where there are plenty of empty seats). Van Niel’s section looks pretty full in the pictures, though. But Van Niel himself admits at least one of the balls wasn’t hit right to him.

All I can say for sure is that these drive the chances up – so the probability of catching four foul balls in a single game is probably a good deal higher than one in a trillion.

A visualization of normal versus fat-tailed distributions

Archimedes: Separating Myth from Science at the New York Times.

Daniel Walsh plays detective with rolling shutter photos: given a picture of a moving propeller, can you tell how fast it was moving?

Dave Richeson uses a kayak to measure the perimeter of a lake.

From Brain Facts, some visualizations of nonlinear systems.

A profile of Aaron Clauset’s research on power laws and terrorism.

Academic doesn’t have a PhD problem. It has an attitude problem.

Gil Kalai givces a solution to auction-based tic tac toe.

the Guardian has a video in which Paul Klemperer talks about geometry and the banking crisis. Surprisingly it’s tropical geometry to the rescue in resource allocation problems, as seen in this paper by Klemperer and Elizabeth Baldwin.

Brian Whitman tells us how music recommendation works and doesn’t work.

From yhat, handwritten digit recognition with node and python.

I asked about a month ago are Amazon rankings Zipfian?

Morris Rosenthal, a self-publishing author, has an interest in this subject for obvious reasons; he’s got some interesting-looking resutls for both paper books and e-books. Roughly speaking, yes; the most interesting thing I notice is that the slope of the rank vs. estimated sales curve (on a log-log scale) is higher both at the head (best-seller) and in the tail of the distribution compared to its bulk. What to make of this, I don’t know.

Chad Orzel, a physicist and author of How To Teach Physics to Your Dog took his own shot at this question a couple years ago.

David Eppstein asks: how many riffles does it take until all permutations are possible?

A riffle shuffle permutation, in the mathematics of shuffling cards, is a permutation of the cards that can be obtained by a single riffle shuffle — that is, you cut the deck into two packets and then interleave the packets. There are distinct riffle shuffles of n cards. For example, consider a five-card deck, which is initially in the order 1, 2, 3, 4, 5. Then a riffle shuffle consists of:

• cutting the deck in one of the six possible ways: 12345/ (no cut), 1234/5, 123/45, 12/345, 1/2345, /12345 (also no cut) where the slash represents the cut.
• riffling. For example look at 123/45. There are possible ways to make a permutation from this – we decide which two slots to put the 4 and the 5 in, and then everything else is forced. For example if we decide that 4 and 5 will go in the second and fourth positions, we must get 14253. In general if we have k cards in the left-hand pile and cards in the right-hand pile, we have $\latex n \choose k$ possible shuffles. Furthermore we can decompose any one of these permutations into two “rising sequences” in exactly one way, so it can come from exactly one cut — with a single exception. That exception is the identity permutation , which we can obtain from any of the n+1 possible cuts — so we must subtract n for the duplications. (If you put probabilities on this it becomes the Gilbert-Shannon-Reeds model.

Eppstein asks how many riffle shuffles it takes for each permutation to have nonzero probability. Since there are outcomes of a single riffle shuffle, in k iterations there are at most possible results. There will actually be less, because there are relations among the permutation subgroup generated by the riffle shuffles. (In less fancy language, there are sequences of different shuffles which give the same result. It’s the pedigree collapse of shuffling.)

Let’s replace this with to make the math easier. Now, there are permutations; this is greater than by a standard bound. So just in order to have possible sequences of shuffles of length k, we have to have , or, taking nth roots of both sides, . Taking base-2 logs, we get .

Eppstein gives a dynamical systems argument that you need at least $\lceil \log_2 n \rceil$ shuffles – and it turns out that that’s enough. This is in comparison to the classic result of Bayer and Diaconis, claiming that you need $3/2 \log_2 n$ shuffles to get a well-shuffled deck.

Dave Richeson tweeted about a puzzle from Futility Closet (original source a Russian mathematical olympiad): can you split the integers 1, 2, …, 15 into two groups A and B, with 13 elements in A and 2 elements in B, so that the sum of the elements of A is the product of the elements of B?

Think about it for a moment. There’s of course the temptation to brute-force it, which is doable, but there’s a more elegant solution.

This got me thinking – when can you split the integers 1, 2, …, n into two groups A and B, where B has two elements, so that the sum of the elements of A is the product of the elements of B?

Say B contains x and y. Then their product is of course xy. The sum of the elements of A is . Setting these equal and rearranging gives

where we’ve added 1 to make the factorization work out – this becomes

.

So the problem is reduced to finding factorizations of n(n+1)/2 + 1, which satisfy two conditions:

• x and y can’t be equal (for specificity we’ll say x < y), and
• x and y are both at most n.

Since we have y ≤ n, we’re going to have x ≥ (n+1)/2 + 1/n. n must be at least 2, so we can just write x ≥ (n/2) + 1. So we’re looking for factors of n(n+1)/2 + 1 in the interval [n/2+1, n]. Here’s some brute-force Python code to find all such solutions:

import math

def solutions(n):
    out = []
    total = n*(n+1)/2+1
    xmin = int(math.ceil(n/2.0) + 1)
    xmax = n
    for x in range(xmin, xmax+1):
        if total % (x+1) == 0:
            y = total/(x+1)-1
            if x < y:
                out.append([x,y])
    return out

def all_solutions(n):
    out = []
    for i in range(2, n+1):
        sols = solutions(i)
        for sol in sols:
            sol.insert(0, i)
            out.append(sol)
    return out

solutions takes an integer n as input and returns pairs [x, y] which are solutions to the problem. For example solutions(17) returns [[10, 13]].
And all_solutions takes an integer N and returns all triples [n, x, y] with which are solutions to the problem — that is, where xy equals the sum of all the integers up to n except for x and y. The first few solutions are:

n	x	y
10	6	7
17	10	13
26	15	21
36	22	28
37	21	31
45	27	36
50	28	43
61	42	43
65	36	57
67	42	52
78	45	66
82	45	73
91	52	78
94	57	76
101	55	91
102	70	73
110	70	85
122	66	111
136	76	120
138	87	108

So it appears that there’s nothing particularly special about the number 15 in the initial puzzle. There are plenty of values n for which you can’t do this, and plenty for which you can. Also, there are values of n for which there are multiple solution pairs (x, y), although not surprisingly they are rare. The smallest such n is 325, for which and are both solutions. In this case $latex n(n+1)/2 + 1 = 52976 = 2⁴ \times 7 \times 11 \times 43$, from which 52976 has (5)(2)(2)(2) = 40 factors. A typical number of this size has about factors. This abundance of factors makes it more likely that 52976 would have two factorizations of the sort we’re looking for. And in fact .

Solutions to this problem appear to have some interesting statistical properties… more on that in a future post.

Simulated car design using genetic algorithms.

From the arXiv:
The Supreme Court is a spin glass.
How should traffic signals be timed on two-way streets?

From the June Notices of the AMS:
Judith R. Goodstein and Donald Babbitt’s article of E. T. Bell and Caltech mathematics between the wars (of Men of Mathematics and Bell numbers fame).
Richard Hoshino and Ken-ichi Kawarabayashi, “Graph Theory and Sports Scheduling”. As you might suspect from the names of the authors, they’re Japanese; the numbers they use in their problem apply to Japanese pro baseball (NPB), and their work has been used in actual scheduling of NPB.

Bryna Kra on mathematics as a toolbox for the sciences in the Chronicle of Higher Education.

Joel Grus can analyze data and has a two-year-old daughter, so naturally he looked at the most boyish and girlish colors and eigenshirts for children’s T-shirts.

Alex Bellos at the Guardian shows us mathematical food items.

William Beaty on the physics behind traffic jams.

Tom Fawcett has a gallery of visualization of results from machine learning classifiers.

Jon McLoone asks is there any point to the 12 times table?

Rafe Kinsey, at the University of Michigan, is teaching a freshman writing course on math, writing, and the world in the fall of 2013.

The boy who loved math: the improbable life of Paul Erdos is an illustrated children’s book.

John Cook on statistical evidence vs. legal evidence.

Gurmeet Manku has a collection of “75 combinatorial puzzles for mathematicians and computer scientists.”.

Celebrities die e at a time. (via Reddit)

From Nautilus magazine: how to insure against a rainy day and taming the unfriendly skies.