So earlier today I was walking along, listening to the Math/Maths Podcast. They mentioned Erdös numbers, as math people are wont to do occasionally. It occurred to me that nobody can get an Erdös number of 1 now — of course — and that at some point in the future, all of Erdös’s collaborators will have died, so it will be impossible to get an Erdös number of 2. So how old, I wondered, is the youngest of Erdös’s collaborators?

The latest birthdate I could find on the Internet for an Erdos collaborator was Csaba Sandor, May 10, 1972.
(This Christian Mauduit, born 6/9/75, is not the Erdos collaborator.) Information about dates of PhDs and such is easier to find, and yields two potential younger collaborators.  Gergely Harcos is one: he started primary school in ’79, university in ’91, and got his PhD in ’03.  Laszlo Koczy got his PhD in ’03; he’s an economist but has some discrete-math interests, so may be the Erdos collaborator. To find these people I took the list of Erdos collaborators by date of first collaboration and started googling names from the bottom until I got tired. This happened pretty quickly, so I can’t guarantee that I’ve found Erdös’s youngest collaborator.

Of course then I got home and came across a similar question for baseball players at sports nation divided. Here the nodes are baseball players, and two players are linked if they faced each other in Major League Baseball play, one as a batter and the other as a pitcher. It’s possible to get from the 19th century to the present day in six steps. This seems about right — twenty years is a rough upper bound for the length of an MLB career, and a regular batter/pitcher will face most pitchers/batters in their league in a given season, so it should be possible to do this in six steps.

Uncovering Ramanujan’s “Lost” Notebook: An Oral History, by Robert Schneider from interviews with George Andrews, Bruce Berndt, and Ken Ono.
I’m looking for a job, in the SF Bay Area. See my linkedin profile.

The Chaos Within Sudoku, by Maria Ercsey-Ravasz and Zoltan Toroczkai; from the Technology Review blog; this paper gives a means of algorithmically rating Sudoku puzzles’ hardness by mapping them onto dynamical systems. David Eppstein comments; he’s previously given this question some thought.

Jeremy Kun has an excellent blog entitled Math ∩ Programming.

Rubik’s Cube Twists Back Into Limelight (and the Times is on it!)

Nate Silver runs down a list of other presidential forecasting models.

Olympics: medals per capita, alternative medal table.

The little book of R for time series

Stanislas Dehaene and Steven Strogatz, How Math Comes to Mind: Intuition, Visualization, and Teaching, 79 minute public lecture given at Princeton in 2011. The story of how Strogatz almost got weeded out of math starts at 29:10. (Audio-only track is also available, and it should hold up that way; it’s just people talking.)

Square root laws for basketball.

I’m looking for a job, in the SF Bay Area. See my linkedin profile.

Which country wins the Olympics? Right now China is in the lead for most medals (73: 34 gold, 21 silver, 18 bronze) and most golds. The USA is second in both categories (71: 30 gold, 19 silver, 22 bronze). In 2008 there was some controversy about whether the ranking should be done by largest total number of medals or largest golds; here’s the table from Wikipedia. If I recall correctly (though it’s surprisingly hard to search for this) non-Americans were saying that the “right” way to do it is by golds, but Americans insisted on doing it by total medals. Not surprisingly the USA had the most total medalists in ’08 (110, to China’s 100) but not the most golds (36, to China’s 51).

But it hardly seems fair to expect, say, France to get as many medals as the USA, simply because they have about one-fifth the population. Shouldn’t their 41 medals in ’08 count for something? In fact they beat the US on a per-capita basis. In the current (2012) Olympics, as of two days ago Slovenia led the medal table per capita, says the New York Times. (This actually isn’t a case of a small country winning one medal; the Slovenes, at that point, had four medals for their two million people.) Medals per capita has up-to-the-minute data; as of this writing New Zealand (one medal per 443,262 people) has pulled ahead of Slovenia, and Grenada (110,821 people; one medal) is in the lead and is quite likely to stay there. Historical data is available as well; since 1984 it’s always been a very small country in the per-capita lead.

But per-capita counting is probably a little bit too aggressive in adjusting high-population countries downwards, because there are some events that have a limit in number of competitors per country. Team sports come to mind; there’s no way the USA will win more than two medals in basketball, despite its dominance. (Of course I’m trying to prop up the USA here! The site’s creator, Craig Nevill-Manning, is a New Zealander.) We could do regression to determine how many medals we’d expect a country of a given size to win, and then judge countries relative to that benchmark.

So here’s a way to put a partial order on countries: country A is “better” at the Olympics as country B at the Olympics if A wins more medals than B and has smaller population. We can plot the medal counts in a scatterplot — see below. The “winners” of the Olympics — and there are many — are all the maxima under this partial order, that is, all the countries for which no smaller country got more medals. Winners therefore include the lowest-population country to win a medal — in ’08, that was Iceland — and the country that won the most medals — that is, the USA. Intermediate between them, in 2008, were the Bahamas, Jamaica, Belarus, Cuba, Australia, Great Britain, and Russia. On the scatter plot below, these are those countries for which, if you draw a vertical line and a horizontal line through the point representing them, there are no points in the upper left quadrant; I’ve drawn those lines for Australia.

So far in 2012 the leaders in this category are China, the USA, Great Britain, Australia, Romania, Hungary, Slovenia, Estonia, and Grenada. (But don’t read too much into the differences between these lists, especially at the small-country end; during the Olympics such a list will be biased towards countries that happen to be good in events that happen early on.) I’ll put out the final results once the Olympics end.

I’m looking for a job, in the SF Bay Area. See my linkedin profile.

Edited to add, 12:29 pm: in this 2012 New York Review of Books article on the pursuit of medals, I found a link to this 2008 Wall Street Journal article on differing schemes of ranking countries, namely the gold-versus-total-medals debate.

If I type “mathematicians are” into Google and let it auto-suggest completions, I get “mathematicians are people too”, “mathematicians are like frenchmen”, “mathematicians are people too pdf”, and “mathematicians are weird”.

The first and third are references to a book Mathematicians Are People, Too: Stories from the Lives of Great Mathematicians
which appears to be a book of stories from the lives of mathematicians, intended for young children.

The second refers to a quote of Goethe: Die Mathematiker sind eine Art Franzosen; redet man mit ihnen, so übersetzen sie es in ihre Sprache, und dann ist es alsobald ganz etwas anderes. (Mathematicians are [like] a sort of Frenchmen; if you talk to them, they translate it into their own language, and then it is immediately something quite different.)

The fourth doesn’t seem to be a reference to anything in particular, but turns up some interesting Google results on how people perceive mathematicians; I’ll let you do your own Googling.

Possible completions for “statisticians are” are: “statisticians are liars”, “statisticians are many lovers”, “statisticians dc area”, “are statisticians scientists”. Apparently the quip about lies, damned lies, and statistics has been rephrased as “liars, damned liars, and statisticians”; “statisticians are many lovers” might be a distortion of “statisticians are mean lovers”. I’m not touching the question of whether statisticians are scientists before coffee.

I’m looking for a job, in the SF Bay Area. See my linkedin profile.

Cycles in human history?

Maximizing the probability of getting a medal in diving.

The most mathematical flag, from Numberphile. (The pictures you’ll want to see are here.)

John D. Barrow asks: How fast can Usain Bolt run? PDF, one-hour lecture on more general topics including this.

The optimal angle of release in shot put, by Alexander Lenz and Florian Rappl: paper at the arxiv, Technology Review blog (It’s not 45 degrees.)

Cosmos: A Three-Movement Choral Suite, by Kenley Kristofferson. (Yeah, I know, it’s not math. Deal with it.)

The Olympic running events are in the following distances: 100m, 200m, 400m, 800m, 1500m, 5000m, 10000m, marathon (42195m, although the original marathon in 1896 was 40km flat).

It’s clear that this sequence is trying to have each race be roughly twice the length of the one before… but there’s a bit of interference from the desire to make the races “round numbers” in base 10. And there are a couple omissions: why is there no 3km race, or 20km race?

In the winter, Speed skating contests a slightly harder to explain sequence: 500m, 1000m, 1500m, 3000m (women only), 5000m, 10000m (men only). This makes a bit more sense, I suppose, if you bear in mind that speed skating is done on a 500 meter track, so the first three are once, twice, and three times around the track. (But then why 1500 meter running — why not 1600, which is four times around the 400 meter track?)

Swimming actually does the best job of sticking to powers of two, racing distances of 50m, 100m, 200m, 400m, 800m (women only), and 1500m (men only). Again, though, it’s 1500 instead of 1600. It’s almost as if they’re trying to avoid 1600m because it’s too close to a mile.

It actually makes some sense that the basic principle is that each race should be twice the length of the one before; presumably the idea is that “twice as long” is long enough to be a different sort of race, but not so much longer that there are people who would be best at some distance that falls in the gaps.

I’m not going to pretend to understand how Olympic cycling races work, because I don’t.

I’m looking for a job, in the SF Bay Area. See my linkedin profile.

More Olympic mathematics: from the arxiv blog, statisticans predict the number of olympic records that will fall at London 2012. The paper is A survival analysis of the duration of Olympic records, by Elliott Hollifield, Victoria Treviño, and Adam Zarn.

Jordan Ellenberg explains the genius of the new (in 2008) gymnastics scoring system. If I may summarize: gymnastics doesn’t naturally have some right wall of performance, so why act like it does?

I’m actually watching the women’s all-around gymnastics final right now. There are eight teams in it, and four pieces of apparatus, so obviously turns have to be taken; therefore at any given time each team will have performed the same number of routines, but not necessarily on the same apparatus. And since different teams are strong on different apparatus, this means that saying “X is ahead of Y” is a bit meaningless. If gymnastics had a bigger following someone would have worked out how to correct for this and tell me who’s really in the lead, given their remaining events and how they’ve performed historically in them. (I had the same thought during the individual medley in swimming yesterday; at some point one person was well behind but the commentators said that they’d probably come back on the last leg because the last leg was their best stroke, and if I recall correctly that turned out to be true.)

Why am I sitting here at nine in the morning watching the Olympics? Because I’m looking for a job, in the SF Bay Area. See my linkedin profile.

Nate Silver asks which Olympic records get shattered.

mages forecasts the winning time in the men’s 100m in the Olympics (9.68 sec).

Dan Graetinnger predicts the Olympic medal counts.

Andrew Hacker’s opinion piece Is Algebra Necessary? has been making the rounds. No comment.

Why isn’t iTunes shuffle random?, from AskDifferent (the StackExchange site for Apple products).

A four-time lottery winner is a Stanford statistics PhD.

A couple series of posts from John Baez: Symmetry and the four dimension one, two, three, four. The Mathematics of Biodiversity eight-part series.

Boolean buddhas.

I’m looking for a job, in the SF Bay Area. See my linkedin profile.

A “Fibonacci prime” is nothing more than a number which is both prime and a Fibonacci number. The indices of the first 33 Fibonacci primes, and the “probable” next 13 (in the probable prime sense), are A001605 in the On-Line Encyclopedia of Integer Sequences. The sequence of such indices begins 3, 4, 5, 7, 11, 13, …; the corresponding Fibonacci numbers are 2, 3, 5, 13, 89, 233, … . As is pointed out in the note at the OEIS, since F_mn is divisible by F_n all further entries in that sequence must be prime. The converse is not true; the first exception is F₁₉ = 4181 = (37)(113).

Are Fibonacci primes rare? To answer this question we need to define “rare”; specifically, if you know a number is a Fibonacci number, does that make it more or less likely to be prime than it would otherwise be? The nth Fibonacci number is roughly φⁿ, so by the prime number theorem the “probability” that the n

Fibonacci number is prime is 1/(n log φ). Integrating, there ought to be about (log n)/(log φ) primes among the first n Fibonacci numbers; inverting, the xth Fibonacci prime should be somewhere around index φ^x.

We can plot the points (1, log(3)), (2, log(4)), (3, log(5)), (4, log(7)), …, (46, log(1636007)), where the y-coordinates are the indices of the Fibonacci primes, and see if they fall roughly on a straight line. The picture is below. If the heuristic above is correct, they should fall on a line of slope log φ, or about 0.48. They actually fall on a line of slope about 0.31. For example, there should be, by the heuristic in the previous paragraph, about (log 1636007)/(log φ) ≈ 30 Fibonacci primes with index less than 1636007; there are actually 46. There are too many Fibonacci primes.

More generally, do Fibonacci numbers have fewer factors than are typical among numbers of their size? Here are factorizations of Fibonacci numbers at mersennus.net. I don’t know the answer to this question.

I’m looking for a job, in the SF Bay Area. See my linkedin profile.

Service on Bay Area Rapid Transit (BART) runs every fifteen minutes on each route; every twenty minutes on evenings and Sundays. Here’s a map of the system. (The lines in red and green don’t run all the time, but that’s not relevant for what I’m about to say.)

The San Francisco city segment (Daly City to Embarcadero) is served by four of the five routes, and so has service by sixteen trains an hour when all those lines are running, between about 6 AM and 7 PM. Here’s a schedule. If you’re standing at, say, 16th Street (which I was a couple hours ago), northbound (Embarcadero-bound) trains depart at

6:11 am (red, i. e. Richmond-bound)

6:17 am (blue, i. e. Dublin-bound)

6:19 am (yellow, i. e. Pittsburg-bound)

6:24 am (green, i. e. Fremont-bound)

and then that pattern repeats every fifteen minutes through 4:11 pm. (Things get complicated slightly by extra trains in the Pittsburg direction in the evening rush.) That is, in a typical hour:

Dublin trains depart at 2, 17, 32, and 47 after the hour;

Pittsburg trains depart at 4, 19, 34, and 49 after the hour, that is, 2 minutes after the Dublin trains;

Fremont trains depart at 9, 24, 39, and 54 after the hour, that is, 5 minutes after the Pittsburg trains;

Richmond trains depart at 11, 26, 41, and 56 after the hour, that is, 2 minutes after the Fremont trains

(and of course Dublin trains depart 6 minutes after the Richmond trains).

(After that there are some extra trains in the direction of Pittsburg/Bay Point for the evening rush hour.)

You’ll notice that these trains are not evenly spaced.
So say I show up at 16th Street at a time chosen uniformly at random between, say, 2 PM and 3 PM, and I want to go to Embarcadero; what is my expected waiting time?

With probability 6/15, the next train heading in that direction is a Dublin train. In these cases, on average I will have to wait 6/2 = 3 minutes.

With probability 2/15, the next train heading in that direction is a Pittsburg train. In these cases, on average I will have to wait 2/2 = 1 minute.

With probability 5/15, the next train heading in that direction is a Fremont train. In these cases, on average I will have to wait 5/2 = 2.5 minutes.

With probability 2/15, the next train heading in that direction is a Richmond train. In these cases, on average I will have to wait 2/2 = 1 minute.

So my average waiting time is (6/15)(3) + (2/15)(1) + (5/15)(2.5) + (2/15)(1) = 2.3 minutes. You could also write this as

and this is an example of a general formula; the numerator is the sum of the squares of the times between different trains, the denominator is twice the period on which the system runs. On average I’ll have to wait 2 minutes and 18 seconds for a train if I just show up without looking at the schedule.

How much worse is this than the optimal spacing? The denominator of that fraction has to be 30; the numerator is the sum of the squares of four numbers that add up to 15. To minimize that sum of squares we want the numbers in the numerator to be as close together as possible. (This is roughly Jensen’s inequality.) Assuming that the inter-train spacings have to be integer numbers of minutes, we’ll go with 3, 4, 4, and 4, and the average wait time ends up being

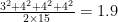
and if we were allowed to not have the spacings be integer numbers of minutes, we could get this down to 1.875 minutes by having trains exactly three minutes and 45 seconds apart.

So BART is costing people who commute within San Francisco 0.425 minutes — or twenty-five and a half seconds — every morning and evening, with this non-optimal train spacing! Or fifty-one whole seconds a day! I suppose this isn’t really worth worrying about, especially since I spent a good half-hour writing this post…

(I haven’t thought hard enough to figure out if there’s some constraint that makes it impossible to space out trains more evenly; in particular that might interact poorly with the spacing on some other interlined segment of the network. It is also possible that this is deliberately done by BART so that people who just show up without looking at a schedule, intending to take the next train to a point within the city, are more likely to end up on Dublin or Fremont trains, as those are the lines that are less used in their East Bay segments; you can see that from this chart of number of people exiting at each station on weekdays and some artihmetic. If so, well done, BART people! If not, well, pretend you meant to do it that way.)

I’m looking for a job, in the SF Bay Area. See my linkedin profile.