Let’s say for some reason that you know and
, for some angle
, and you need to figure out what
is. Let’s say, furthermore, that you live in some benighted age which doesn’t have calculators or even trigonometric tables.
There are a few approaches to this. One is what I did in my “Pythagoras goes linear” post. We can fit a linear model to the points
where the $\theta_i$ range over an arithmetic sequence with endpoints 0 and $\latex \pi/2$, namely
The model you get out is quite simple:
This is actually just a few lines of R.
n = 10^6 theta = (c(0:n))*pi/(2*n); x = cos(theta); y = sin(theta); summary(lm(theta~x+y))
I’ll save you the output, but be impressed: r2 = 0.9992$, and the mean square error is 0.0126 radians or 0.72 degrees. So we can write , in radians. In degrees this is
.
For example, say you have an angle with — the smaller angle of a 5-12-13 right triangle. Then we get
. In fact
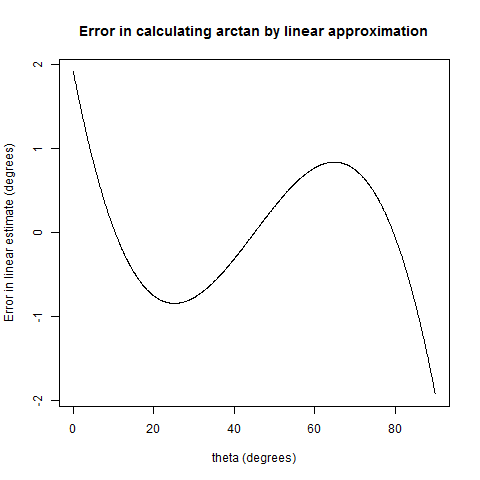
— we’re not off by much! And the error is never more than a couple degrees, as you can see in the plot below.
This was inspired by a post by Jordan Ellenberg that I came across recently: How to compute arctangent if you live in the 18th century, which refers back to my Pythagoras goes linear. A better approximation, although nonlinear, is
where . This is essentially a simplification of the rule that Ellenberg’s source (Hugh Worthington’s 1780 textbook, The Resolution of Triangles) gives, which can be translated into our notation as
Applying this to our test angle with
, we get
radians, while in truth
.
This formula is so nice that I can’t help but suspect there’s a simple derivation. Any takers?
I assume you mean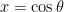 and
and 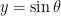 .
.
Here’s one way you could invent that approximation: you recall that

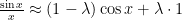
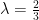 makes the
makes the 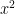 terms equal, and then rearranging yields
terms equal, and then rearranging yields

and you’d like to know more precisely where in that range the middle function falls. Maybe you make the guess that it’s close to a convex combination of the two functions on either side:
The choice
as desired.
(Sorry for any latex errors; there’s no preview, alas.)
This looks like it’s related to multivariable Padé approximants. Let me take quick stab at it, apologies for no LaTeX.
Assume that there is some approximating function of the form
t ~= (a0+a1*x+a2*y)/(1+b1*x+b2*y).
Multiply across and rewrite in terms of theta as:
t ~= a0 + (a1-b1*t) sin t + (a2-b2*t) cos t
Now, replace the trigonometric function with their series representations:
t ~= a0 + (a1-b1*t)[t – t^3/6 +O(t^5)] + (a2-b2*t)[1-t^2/2+t^4/24+O(t^6)]
Collecting terms up to t^4, we have
t ~= (a0+a2)t^0 + (a1 – b2) t + (-a2/2 – b1) t^2 +(-a1/6 + b2/2) t^3 + (a2/24 + b1/6)t^4
Now just match the powers and boom, five equations in five variables. Mathematica gives me a1 -> 3/2, b2 -> 1/2, and all others 0. Therefore, the final function form would be:
t ~= (3y/2)/(1+x/2) ~= 3y/(2+x)
and we’re done. Padé approximants are quite nifty and have cool applications. My personal favorite is using exp(x) ~= (2+x)/(2-x) to quickly calculate interest rates in my head.
logosintegralis
Apologies, the x and y were switched in my last formula. As the first commenter pointed out, it should be x=cos t and y = sin t. I stand by the rest of the derivation, though.
For most people, being overweight isn’t the
actual problem but rather a symptom of a more serious underlying problem.
Order your pack of Nidora as a weight loss and feel the difference when you try it up to 1 month.
Diet Houston, which consists of fat burning hormones, is one of the many solutions available.