I’ve been on a bit of an inadvertent hiatus from blogging – stuff picked up at my day job and then I got married. Time to get back into the swing of things.

I went to the DMV this morning. (That’s the “Department of Motor Vehicles”, for non-American readers; this is the government agency that handles vehicle registration and driver licensing.) It was “fun”, by which I mean not fun, but I was reminded of this clip from Seinfeld (transcript here):

JERRY: Elaine, what percentage of people would you say are good looking?

ELAINE: Twenty-five percent.

JERRY: Twenty-five percent, you say? No way! It’s like 4 to 6 percent. It’s a twenty to one shot.

ELAINE: You’re way off.

JERRY: Way off? Have you been to the motor vehicle bureau? It’s like a leper colony down there.

ELAINE: So what you are saying is that 90 to 95 percent of the population is undateable?

JERRY: UNDATEABLE!

ELAINE: Then how are all these people getting together?

JERRY: Alcohol.

Jerry is implying here that the people at the DMV are a good sample of the general population. This seems like a reasonable assumption, although of course we can quibble:

• rich people are more likely to own multiple cars, which means they have to go the DMV more often to handle car-registration-related business;
• similarly, poor people are more likely to not have cars at all and perhaps not even be licensed drivers. Since Seinfeld is set in New York, which has low car ownership rates, this is especially true, although it might be counteracted by the fact that public transit is better in the more wealthy parts of that city;
• results should vary by time of day, day of week, and DMV office

Still, it kept me amused while I waited.

From Deathsplanation, How tall is an alpaca? (and how long did people live in the past?)

From the Aperiodical, how to win at (the UK game show) Pointless.

Igor Pak has a collection of attempts to define combinatorics and a blog post on the subject.

From the MAA, some beautiful drawings of Platonic solids from the 16th-century printmaker Wenzel Jamnitzer.

From the Telegraph, Quants: the maths geniuses running Wall Street.

George Hart on making music with Mobius strips (following Dmitri Tymoczko).

Andrew Gelman and Kevin O’Rourke ask how statisticians pick their methods.

Carlos Futuri’s cartographical map projections.

OpenSignal on how phone batteries measure the weather (via Hacker News)

Hanging Hyena on unbeatable words in Hanging with Friends.

Emily Singer for Quanta magazine: In Natural Networks, Strength in Loops.

Hannah Fry on why everyone is more popular than you.

Jiri Matousek has a collection of Thirty-three miniatures: Mathematical and algorithmic applications of linear algebra

A Quora question, What kind of math do you use in your work?

Let’s say for some reason that you know and , for some angle , and you need to figure out what is. Let’s say, furthermore, that you live in some benighted age which doesn’t have calculators or even trigonometric tables.

There are a few approaches to this. One is what I did in my “Pythagoras goes linear” post. We can fit a linear model to the points

where the $\theta_i$ range over an arithmetic sequence with endpoints 0 and $\latex \pi/2$, namely

The model you get out is quite simple:

This is actually just a few lines of R.

 n = 10^6
 theta = (c(0:n))*pi/(2*n);
 x = cos(theta); y = sin(theta);
 summary(lm(theta~x+y))

I’ll save you the output, but be impressed: r² = 0.9992$, and the mean square error is 0.0126 radians or 0.72 degrees. So we can write , in radians. In degrees this is .

For example, say you have an angle with — the smaller angle of a 5-12-13 right triangle. Then we get . In fact — we’re not off by much! And the error is never more than a couple degrees, as you can see in the plot below.

This was inspired by a post by Jordan Ellenberg that I came across recently: How to compute arctangent if you live in the 18th century, which refers back to my Pythagoras goes linear. A better approximation, although nonlinear, is

where . This is essentially a simplification of the rule that Ellenberg’s source (Hugh Worthington’s 1780 textbook, The Resolution of Triangles) gives, which can be translated into our notation as

Applying this to our test angle with , we get radians, while in truth .

This formula is so nice that I can’t help but suspect there’s a simple derivation. Any takers?

Cathy O’Neil asks if lawmakers should use algorithms.

Daina Taimina gave a talk at TEDxRiga, Crocheting adventures in hyperbolic planes.

Corey Chivers gave a talk on competitive data science (Kaggle) using R and Python.

Colm Mulcahy has another nice mathematical card trick.

Mark Pearson on average distances to airports.

Jennifer Ouellette on the mathematics of learning language.

Geoffrey de Smet on false assumptions for vehicle routing.

From embed.ly, visualizing reddit discussions.

What’s the theoretical limit for the rate of success of predicting wins and losses in NHL games?

Some statistics from Tim Day’s experience solving Project Euler problems.

Alexander Klotz examines the gravity tunnel in a non-uniform Earth.

Carl Rasmussen and Christopher Williams’ book Gaussian Processes for Machine Learning is available free online.

Joseph Rickert summarizes Nate Silver’s appearance at this year’s Joint Statistical Meetings.

From Wired a couple years back, Jason Fagone, Teen Mathletes Do Battle at Algorithm Olympics (i. e. the IOI).

David Bau’s conformal map viewer.

Predicting the NFL using Twitter, by Shiladitya Sinha, Chris Dyer, Kevin Gimpel, and Noah A. Smith.

Apologies if you just got an e-mail consisting of a bunch of links with no annotation. I hit the wrong button.

From James Harvey: The Powerball Jackpot is $425m. Should you play? (It’s too late for you to care – I’m writing this at 7:51 PM Pacific time, and the drawing is at 7:59 – but if nobody wins, you might care on Saturday, with a bigger number.) Harvey’s conclusion: it basically never makes sense to play, because as the jackpot goes up the likelihood of having to split it also goes up. But he’s still in it, for the entertainment value.

I’ve got some tickets, too, because some coworkers went in on a pool, and I don’t want to be the sucker who has to go to work tomorrow.

Roberto Tamassia at Brown is the editor of the Handbook of Graph Drawing and Visualization, which you can read online.

David Eppstein on how to play Planarity.

Edmund Harriss wrote a blog post on “Form Follows Functions”, a teaser for these notes of the same name graphically exploring how changes in functional forms translate into changes in the corresponding graphs.

Chris Stucchio on Mechanical Turk and error correcting codes.

Insight Data Science on the transition from PhD to data scientist (via Hacker News).

Miguel Rios at the official twitter blog on visualizing volume data from twitter; the corresponding paper is Miguel Rios and Jimmy Lin, “Visualizing the ‘Pulse’ of World Cities on Twitter. Of particular interest is Twitter data from Riyadh, where prayer times and Ramadan are immediately observable.

Steve Staude at Fangraphs did a two-part analysis of forecasting strikeout rates in batter-pitcher matchups from the averages for the batter and the pitcher: part one, part two. It’s a hell of a lot better than using data on the individual matchup between batter X and pitcher Y, which is plagued with notoriously small sample sizes.

From Cathy O’Neil: The Stacks Project gets ever awesomer with new viz
Analyzing the complexity of the Stacks Project graphs; from Jordan Ellenberg, How much is the Stacks Project graph like a random graph? (The Stacks project is an online textbook of algebraic geometry, but these posts are not about algebraic geometry.)

Timo Bingmann has constructed some visualizations/audibilizations of sorting; Brady Haran has similar video in his Computerphile channel.

During a baseball game today, heard a commercial for Domino’s Pizza claiming that they have 34 million different pizzas. This is apparently a claim that Domino’s started making in saying that they shouldn’t be forced to list calorie counts: see the Washington Post from June 2012.

In any case, I wondered where they got that number. From their online ordering tool I find:

• on the first page (size & crust): 10 combinations of size and crust;
• on the second page (cheese & sauce): six different amounts of cheese (none, light, normal, extra, double, triple) and thirteen sauce choices: four kinds of sauce each in three different amounts, or none;
• on the third page, 25 different toppings, each of which you can order in six different amounts (none, light, normal, extra, double, triple).

The “34 million” number is presumably 2²⁵ = 33,554,432 (yes or no for each topping), but a more accurate calculation of the number of possible pizzas is or about $2.2 \times 10^{22}$. Call this number . And even that’s ignoring that you can make independent choices for the two halves of your pizza – so if we really wanted to inflate the number, there are possible pizzas, where the pizzas are just pairs of choices for the two halves. This is around .

But nobody would have believed that. And how many of those pizzas are any good?

Brian Hayes on crinkly curves.

Eric Colson at Strata 2013 on Stitch Fix’s clothes recommendation algorithm.

Andrew Gelman at Slate on multiple comparisons

Priceonomics on prisoners and the prisoner’s dilemma.

Neal Wagner has posted preprints of Knuth volume 4A (“Combinatorial Algorithms”).

Randy Zwitch has a tutorial on the scientific programming language Julia.

Patrick Juola wrote a guest post at Language Log on how Robert Galbraith was outed as J. K. Rowling and then Geoff Pullum wrote about Juola; see also the Chronicle (of Higher Ed, not San Francisco). Here’s Juola’s web page and long paper/short book “Authorship Attribution”.

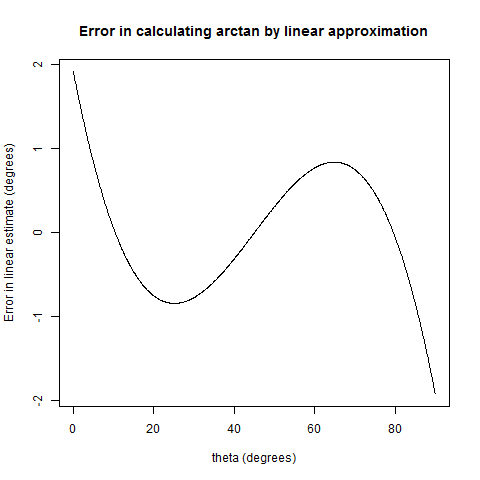
Here’s another brute-force number theory puzzle, in the spirit of the Russian puzzle I looked at a couple weeks ago. From what would Martin Gardner tweet: “Two triangles share one angle but have six different side lengths (all whole numbers between 1 and 9). Find those lengths.”

Do we expect such triangles to exist? Well, clearly there are lots of different-sized right triangles, which share an angle. To take the smallest possible example, 3-4-5 and 6-8-10 are both the sides of right triangles, and they share an angle. But sadly, 10 is too large…

This is a bit tricky to think about, because the angles of an integer-sided triangle aren’t going to be anything nice. So instead of looking at the angles themselves let’s look at their cosines. Given a triangle with sides having lengths (a, b, c), the angle C, opposite the side of length c satisfies

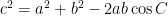
which we can rearrange to give

This is just the law of cosines from “high school trigonometry”, which is a generalization of the Pythagorean theorem to non-right-angled triangles.

So now the search for a solution is just bookkeeping. Let’s look at all the possible triplets (a, b, c) of distinct integers that could be the sides of a triangle. For the sake of keeping things canonical, let’s force . The triangle inequality says that , or , so we get . Furthermore we can see that a must be at least 4, since each of those four inequalities is strict. So we loop over all those possible triples and store them in a Python dictionary according to the cosines of their angles. The following code will ask for an upper bound on the side lengths and carry out the search.

#Import some useful data structures.
from collections import defaultdict
from sets import Set

#Greatest common divisor (by the Euclidean algorithm).  For reducing fractions.
def gcd(a,b):
    while b:
        a, b = b, a%b
    return a

#Takes as input the three sides of a triangle;
#Outputs red_num, red_den such that red_num/red_den is the cosine of the angle opposite the first side given
#as a fraction in lowest terms
def cosine_law(c, a, b):
    raw_num = (-c**2 + a**2 + b**2)
    raw_den = (2*a*b)
    g = gcd(raw_num, raw_den)
    red_num = raw_num/g
    red_den = raw_den/g
    return red_num, red_den

out = defaultdict(set)

maxn = int(raw_input("Largest side to allow? ")) + 1

#Loop over possible triples a, b, c with a > b > c > a-b
#(i. e. in decreasing order and satisfying the triangle inequality)
#and add the cosines of their angles to the dictionary out
for a in range(4, maxn):
    for b in range(-int(-a/2), a):
        for c in range(a-b+1, b):
            if gcd(gcd(a,b),c) == 1:
                cosA = cosine_law(a,b,c)
                cosB = cosine_law(b,a,c)
                cosC = cosine_law(c,a,b)
                #store with vertex first, then larger of two second
                out[cosA].add((a,b,c))
                out[cosB].add((b,a,c))
                out[cosC].add((c,a,b))

#Look through out for pairs of triangles which share an angle
#and have all three sides different.
numsols = 0
for key in out:
    if len(out[key]) >= 2:

       triangles = list(out[key])
       for i in triangles:
           for j in triangles:
               sides = Set([i[0], i[1], i[2], j[0], j[1], j[2]])
               if len(sides) == 6 and i[0] >= j[0]:
                   #print key, i, j
                   numsols = numsols+1

And if we input 9 when it asks for that largest side the output is precisely

(11, 16) (6, 8, 7) (3, 4, 2)

The 2-tuple is the rational number 11/16, the cosine of the angle that these triangles have in common. The triplets represent triangles with an angle , with the side opposite that angle listed first. So the angle opposite the side of length 6 in a 6-7-8 triangle and the angle opposite the side of length 3 in a 2-3-4 triangle both have cosine $11/16$; they are both angles of $\cos^{-1} 11/16$, or about 46.6 degrees.

This leads naturally to the question: are such pairs of triangles rare? The answer is “not at all”. There are 30 solutions to this problem with all sides under 15, 951 with all sides under 30, and 81,014 with all sides under 100.

In fact, heuristically, we expect lots of such solutions. The number of different integer triangles with all their sides less than n is on the order of n³. From the law of cosines, the angles of these triangle will have cosines that are rational numbers with numerator and denominator on the order of n²; there are n⁴ such different numbers. We can wave our hands and say the magic words birthday problem; since the number of possible cosines is much greater than the square root of the number of angles we need to find cosines for, if everything happens “at random” there ought to be lots of collisions — and indeed there are.