A week ago I wrote a post on bitwise set trickery in which I asked a question from James Tanton: how many subsets S of {1, 2, …, 10} have the property that S and S+2 cover all the numbers from 1 to 12? To solve this is a one-liner in R. Slightly generalizing, we can replace 10 by n:
library(bitops)
g = function(n){sum(bitOr(0:(2^n-1), 4*(0:(2^n-1))) == (2^(n+2)-1))}
Then it’s easy to compute g(n) for n = 1, 2, …, 20:
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| g(n) |
0 |
1 |
1 |
1 |
2 |
4 |
6 |
9 |
15 |
25 |
| n |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| g(n) |
40 |
64 |
104 |
169 |
273 |
441 |
714 |
1156 |
1870 |
3025 |
and if positive integers are at least your casual acquaintances you’ll recognize a lot of squares here, and in particular a lot of squares of Fibonacci numbers:
The numbers in between the squares are a little trickier, but once we’re primed to think Fibonacci it’s not hard to see
So this leads to the conjecture that
for positive integers $n$. If you’re allergic to cases you can write this as
So how to prove these formulas? We can explicitly list, say, the g(8) = 9 sets that we need.
sets = function(n){
indices = which(bitOr(0:(2^n-1), 4*(0:(2^n-1))) == (2^(n+2)-1))-1; #like the bit trickery above
for (i in 1:length(indices)) {
print(which(intToBits(indices[i]) == 01)) #convert from integer to vector of its 1s
}
}
(The “-1” is because lists in R are 1-indexed.) Then, for example, sets(9) outputs the fifteen sets
1 2 4 5 8 9
1 2 3 4 5 8 9
1 2 5 6 8 9
1 2 3 5 6 8 9
1 2 4 5 6 8 9
1 2 3 4 5 6 8 9
1 2 3 4 7 8 9
1 2 4 5 7 8 9
1 2 3 4 5 7 8 9
1 2 3 6 7 8 9
1 2 3 4 6 7 8 9
1 2 5 6 7 8 9
1 2 3 5 6 7 8 9
1 2 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9
and now we examine the entrails. Each row consists of a subset S of {1, … 9} such that, when we take its union with S + 2, we get all the integers from 1 up to 11. Now when we add 2 to every element of S, we don’t change parity, so it makes sense to look at even and odd numbers separately. If we extract just the even numbers from each of the sets, we get {2, 4, 8}, {2, 6, 8}, or {2, 4, 6, 8}, each of which occurs five times; if we extract just the odd numbers we get {1, 5, 9}, {1, 3, 5, 9}, {1, 3, 7, 9}, {1, 5, 7, 9} or {1, 3, 5, 7, 9}, each of which occurs three times. Every possible combination of one of the even subsets with one of the odd subsets occurs exactly once!
What to make of this? Well, in order for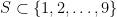 
to satisfy 
, we must have that S contains 2; at least one of 2 or 4; at least one of 4 or 6; at least one of 6 or 8; and 8. Similarly, looking at just the odd numbers, S must contain 1; at least one of 1 or 3; at least one of 3 or 5; at least one of 5 or 7; at least one of 7 or 9; and 9. And 
will satisfy the overall condition if and only if its even part and its odd part do what they need to do; there’s no interaction between them.
So now what? Consider the set in bold above; call it S. Its even part is {2, 4, 8} and its odd part is {1, 5, 7, 9}. We can take the even part and divide everything by 2 to obtain a set T = {1, 2, 4}; we can take the odd part, divide through by 2, and round up to get U = {1, 3, 4, 5}. The conditions transform similarly; in order for 
to satisfy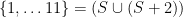 
, we have to have that:
- the set T, obtained from S by taking its even subset and dividing through by 2, contains 1; at least one of 1 or 2; at least one of 2 or 3; at least one of 3 or 4; and 4;
- the set U, obtained from S by taking its odd subset and dividing through by 2, contains 1; at least one of 1 or 2; at least one of 2 or 3; at least one of 3 or 4; at least one of 4 or 5; and 5.
Of course it’s easier to say that T is a subset of {1, 2, 3, 4} containing 1, 4, and at least one of every two consecutive elements, and U is a similar subset of {1, 2, 3, 4, 5}. So how many subsets of {1, 2, 3, …, n} contain 1, n, and at least one of every two consecutive elements?
This is finally where the Fibonacci numbers come in. It’s easier to count possible complements of T. If T satisfies the condition given above, then its complement with respect to {1, 2, …, n} is a subset of {2, 3, …, n-1} containing no two consecutive elements. Call the number of such sets f(n). For n = 3 there are two such subsets of {2}, namely the empty set and {2} itself; for n = 4 there are three such subsets of {2, 3}, namely the empty set, {2}, and {3}. So f(3) = 2, f(4) = 3. Now to find f(n) if n > 4. This is the number of subsets of {2, 3, …, n-1} which contain no two consecutive elements. These can be divided into two types: those which contain n-1 and those which don’t. Those which contain n-1 can’t contain n-2, and so are just subsets of {2, 3, …, n-3} which contain no two consecutive elements, with n-1 added. There are f(n-2) of these. Those which don’t contain n-1 are just subsets of {2, 3, …, n-2} with no two consecutive elements; there are f(n-1) of these. So f(n) = f(n-1) + f(n-2); combined with the initial conditions we see that f(n) is just the nth Fibonacci number.
So we can finally compute g(n). For a set S to satisfy the condition defining g(n) — that is, to have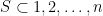 
and $S \cup (S+2) = {1, 2, \ldots, n+2}$ — we have to have that the corresponding 
is a subset of 
containing no two consecutive elements, and the corresponding 
is a subset of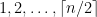 
containing no two consecutive elements. The number of ways to do this is exactly 
, which is what we wanted.
I’m looking for a job, in the SF Bay Area. See my linkedin profile.
as a function of n. Differentiating with respect to n gives 
; this is zero when 
. So if you only have two coins, you want a one-cent coin and a (√ k)-cent coin. Then on average you’d need (√ k)/2 pennies and (√ k)/2 n-cent coins, or a total of √k coins, when making change.
God plays dice 
